北师大版七年级英语七年级数学（上册） 电子课本可以方便大家随时随地预习或复习课本知识，为此，我们找到了北师大版七年级英语（上册） 新教材电子书教材的全部内容，以高清图片的形式呈现给大家，希望能够提高大家的学习效率。

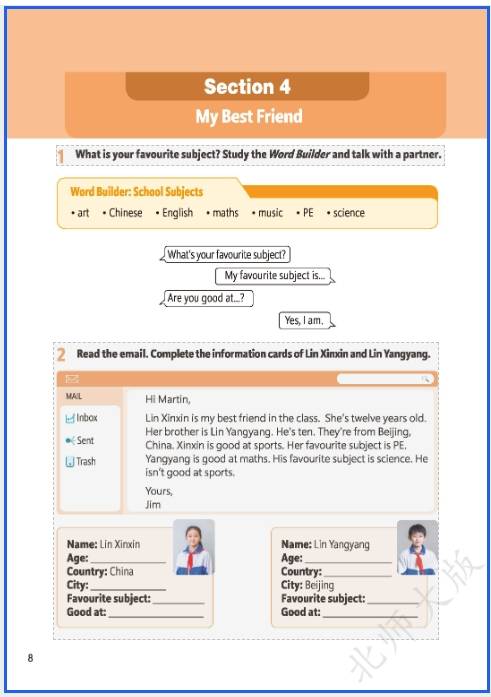
如需全套电子课本PDF版，请关注公众号“桃李文库”回复：“电子课本”

北师大版七年级英语（上册） 新教材电子课本在线阅读（此为截图版，获取是高清版）

数学思维并非天生具备，而是通过系统性训练、针对性思考和生活化应用逐步培养的。它核心包括 “逻辑推理、抽象建模、发散创新、精准计算” 四大能力，以下将从 “训练原则、具体方法、不同学段重点” 三个维度，提供可落地的训练方案。

一、数学思维训练的核心原则：拒绝 “死记硬背”，强调 “理解本质”

数学思维的本质是 “用数学方法解决问题”，训练时需遵循以下原则，避免陷入 “刷题无效” 的误区：

1. “慢思考” 优于 “快刷题”：不追求做题数量，而是每做一道题后追问 “为什么这么做”“还有别的方法吗”“如果条件变了怎么办”。
2. “过程重于结果”：关注解题的逻辑推导过程，而非仅看答案对错。比如做应用题时，要能说清 “第一步求什么、为什么求这个、依据是什么”。
3. “生活化联结”：将抽象的数学概念与生活场景结合，理解其 “实际意义”—— 比如用 “分蛋糕” 理解分数，用 “路线规划” 理解几何图形。
4. “主动纠错”：建立 “错题本”，但重点不是抄题，而是分析 “错误类型”（是概念不清？逻辑断层？还是细节遗漏？），并写出 “正确思路推导”。

二、通用数学思维训练方法：四大核心能力的针对性训练

1. 逻辑推理能力：从 “因果明确” 到 “链条完整”

逻辑推理是数学的 “骨架”，分为演绎推理（从一般到特殊，如 “因为平行四边形对边相等，所以长方形对边相等”）和归纳推理（从特殊到一般，如通过多个 “三角形内角和” 的测量，总结出 “三角形内角和为 180°”）。 训练方法：

• “说题” 训练：做完题后，试着 “把解题思路说给别人听”。如果能清晰表达每一步的 “因” 与 “果”，说明逻辑链完整；若卡壳，就是逻辑断点，需重点补全。 例：计算 “\(1+3+5+7+9\)”，不仅要说出 “结果是 25”，还要说清 “可以用‘（首项 + 末项）× 项数 ÷2’的公式，因为这是等差数列求和，首项 1、末项 9、项数 5，所以（1+9）×5÷2=25”。
• “反向提问” 训练：针对公式、定理，提出 “如果条件不满足，结论还成立吗” 的问题。 例：学了 “三角形两边之和大于第三边”，可以问 “如果两边之和等于第三边，能围成三角形吗？”（实际操作：用 3cm、3cm、6cm 的小棒摆一摆，发现只能摆成一条直线，从而理解 “大于” 的必要性）。
• 趣味逻辑题：通过数独、数阵、逻辑推理题（如 “甲、乙、丙三人中谁是冠军” 的排除法问题）训练严谨性。

2. 抽象建模能力：从 “具体问题” 到 “数学符号”

抽象建模是 “把生活中的实际问题，转化为数学式子或图形” 的能力 —— 这是解决应用题、综合题的核心。 训练方法：

• “翻译” 训练：把应用题的 “文字描述” 转化为 “数学语言”（符号、图形、表格）。 例：“小明有 5 个苹果，妈妈又买了 3 个，现在一共有多少个？” 翻译步骤：① 明确 “已知量”（5 个、3 个）；② 明确 “数量关系”（原有 + 新增 = 现有）；③ 转化为算式 “5+3=？”。 进阶例：“一辆汽车每小时行 60 千米，从 A 地到 B 地行了 2.5 小时，返回时速度提高到 75 千米 / 小时，返回需要几小时？” 翻译：① 画线段图表示 A、B 两地距离；② 用公式 “路程 = 速度 × 时间” 求距离（60×2.5）；③ 再用 “时间 = 路程 ÷ 速度” 求返回时间。
• “一题多境” 训练：用同一个数学模型，设计不同的生活场景，理解模型的通用性。 例：围绕 “乘法模型（总量 = 单量 × 数量）”，设计场景：
• 购物：1 支笔 5 元，买 4 支需要多少元？（单量 = 单价，数量 = 支数）
• 工程：1 小时修 30 米路，修 5 小时修多少米？（单量 = 效率，数量 = 时间）
• 行程：每分钟走 80 米，走 6 分钟走多少米？（单量 = 速度，数量 = 时间）。

3. 发散创新能力：从 “唯一解” 到 “多思路”

数学不是 “只有一种解法”，发散思维能让你在遇到复杂问题时 “灵活破局”，核心是 “不局限于常规思路，尝试从不同角度切入”。 训练方法：

• “一题多解” 训练：针对同一道题，要求用 2 种及以上方法解答，并对比 “哪种更简便”。 例：计算 “12×15”：
• 方法 1（常规乘法）：12×15=180；
• 方法 2（拆数法）：12×(10+5)=12×10+12×5=120+60=180；
• 方法 3（凑整法）：(10+2)×15=10×15+2×15=150+30=180；
• 方法 4（倍数法）：12×15=6×(2×15)=6×30=180。 通过对比，理解 “凑整法更简便”，培养 “优化思维”。
• “一题多变” 训练：改变题目中的一个条件，观察 “解法会发生什么变化”，理解 “条件与解法的关联”。 例：原题 “小明有 10 块糖，比小红多 3 块，小红有几块？”（解法：10-3=7）； 变题 1：“小明有 10 块糖，小红比小明多 3 块，小红有几块？”（解法：10+3=13）； 变题 2：“小明和小红一共有 17 块糖，小明有 10 块，小红有几块？”（解法：17-10=7）。 通过 “变条件”，避免 “机械套公式”，理解 “数量关系的本质”。
• “开放性问题” 训练：设计 “答案不唯一” 的问题，鼓励多角度思考。 例：“用 1、2、3、4 这四个数字，组成两位数乘两位数的算式，哪个算式的积最大？”（需要尝试不同组合：41×32=1312，42×31=1302，34×21=714…… 最终得出 41×32 最大）。

4. 精准计算能力：从 “粗心失误” 到 “流程严谨”

计算是数学思维的 “载体”—— 即使思路正确，计算错误也会导致结果归零。精准计算不是 “速度快”，而是 “步骤规范、结果准确”。 训练方法：

• “流程化” 计算：制定固定的计算步骤，避免跳步。以 “小数乘法” 为例，流程：① 先按整数乘法计算；② 数出两个因数的小数位数总和；③ 在积的末尾从右向左数出对应位数，点上小数点。 例：计算 “2.5×0.4”：① 25×4=100；② 因数共 2 位小数；③ 100 从右数 2 位，点小数点得 1.00，化简为 1。
• “分层” 验算：不同题型用不同验算方法，提高效率：
• 加减法：交换加数位置再算（如 35+27=62，验算 27+35=62）；或用和减一个加数（62-35=27）。
• 乘除法：乘法用除法验算（12×5=60，验算 60÷5=12）；除法用乘法验算（60÷5=12，验算 12×5=60）。
• 方程：把解代入原方程，看左右是否相等（如 2x+3=7，解 x=2，代入：2×2+3=7，左右相等）。
• “针对性” 纠错：统计自己的计算错误类型（如 “符号错”“小数点错”“公式记错”），每天集中练 10 道对应题型，强化薄弱点。

三、不同学段的数学思维训练重点

1. 小学阶段（1-6 年级）：以 “具象到抽象过渡” 为核心

小学是思维启蒙的关键期，重点是 “通过实物、操作理解概念，培养数感、空间观念”。

• 低年级（1-2 年级）：用 “实物操作” 理解数与运算 —— 比如用小棒摆 “10 以内加减法”，用积木理解 “立体图形”，用计数器理解 “数位（个位、十位）”。
• 中高年级（3-6 年级）：从 “实物” 转向 “模型”—— 比如用 “线段图” 解应用题，用 “方格纸” 理解 “面积”，用 “列表法” 解逻辑推理题（如 “鸡兔同笼”：列表枚举鸡和兔的数量，计算脚数是否匹配）。
• 推荐训练：24 点游戏（训练速算和发散思维）、图形拼组（如用七巧板拼长方形、三角形，培养空间观念）、应用题 “说数量关系”。

2. 初中阶段（7-9 年级）：以 “逻辑推理和代数建模” 为核心

初中数学从 “算术” 转向 “代数” 和 “几何”，重点是 “用符号表达关系，用逻辑证明几何性质”。

• 代数部分：训练 “用字母表示数” 的抽象能力 —— 比如从 “具体数字的方程（2x=4）” 到 “含参数的方程（ax+b=c）”，理解 “字母可以代表任意数”；用 “方程模型” 解复杂应用题（如行程、工程、利润问题）。
• 几何部分：训练 “演绎推理” 能力 —— 比如证明 “三角形全等” 时，要严格遵循 “已知→依据定理→结论” 的逻辑链，不能凭 “看起来全等” 下结论；用 “辅助线” 转化问题（如求梯形面积时，添加辅助线转化为平行四边形和三角形）。
• 推荐训练：几何证明题 “倒推法”（从结论出发，思考 “要证这个结论，需要什么条件”）、代数题 “多解法对比”、错题本 “标注错误逻辑点”。

3. 高中阶段（10-12 年级）：以 “抽象建模和综合应用” 为核心

高中数学更抽象（如函数、导数、立体几何），重点是 “将复杂问题转化为数学模型，综合运用多知识点解题”。

• 函数部分：训练 “数形结合” 思维 —— 比如通过函数图像理解 “单调性、奇偶性”，用 “图像法” 解不等式（如 | x-1|>2，画出图像直接看解集）。
• 立体几何：训练 “空间想象” 和 “向量建模” 能力 —— 比如用 “空间向量” 解决 “线面垂直、二面角” 问题，将几何问题转化为代数计算。
• 综合题：训练 “拆解问题” 能力 —— 把压轴题（如导数与函数、数列与不等式）拆成 “几个小问题”，逐一突破，再整合答案。
• 推荐训练：“一题多解”（如数列求和可用公式法、错位相减法、裂项相消法）、“专题总结”（如总结 “求函数值域的 8 种方法”）、“模拟题压轴题拆解”。

四、生活化的数学思维训练：让思维 “用起来”

数学思维不止于做题，更要融入生活，让孩子理解 “数学有用”：

• 购物时：让孩子算 “总价”“折扣”（如 “打八折的商品，原价 100 元，现价多少”），理解 “百分数的应用”。
• 整理房间时：让孩子 “分类整理” 玩具（按颜色、大小、类型），理解 “分类思想”（数学中的集合概念）。
• 旅行时：让孩子规划 “路线”（最短路径）、计算 “行程时间”（路程 ÷ 速度），理解 “几何与行程模型”。
• 做饭时：让孩子 “按比例分配” 食材（如 “做蛋糕需要 2 份面粉、1 份糖，现有 400 克面粉，需要多少糖”），理解 “比例关系”。

总结：数学思维训练的关键

数学思维不是 “天赋”，而是 “刻意练习” 的结果 —— 它需要：

1. 从 “理解本质” 出发，拒绝死记硬背；
2. 从 “规范流程” 入手，避免粗心失误；
3. 从 “多思多练” 积累，通过一题多解、一题多变拓展思路；
4. 从 “生活应用” 落地，让数学成为解决问题的工具。

坚持以上方法，不仅能提高数学成绩，更能培养 “严谨、灵活、创新” 的思维品质 —— 这才是数学学习的核心价值。