2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025新

西南大学版五年级数学（上册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

如需全套电子课本PDF版，请关注公众号“桃李科普”回复：“电子课本”

西南大学版五年级数学（上册）电子课本在线阅读

五年级数学答题方式与规范指南

一、核心题型分类及答题方式

五年级数学题型主要分为计算题、填空题、选择题、判断题、应用题五大类，不同题型的答题逻辑和规范重点存在差异，需针对性应对。

（一）计算题：“算理先行，步骤完整”

计算题是基础题型，占分比高（约 30%-40%），核心考查运算能力，答题关键是 “写清步骤、标注关键、验证结果”。

1. 口算题：直接写结果，注重 “快速定位算理”

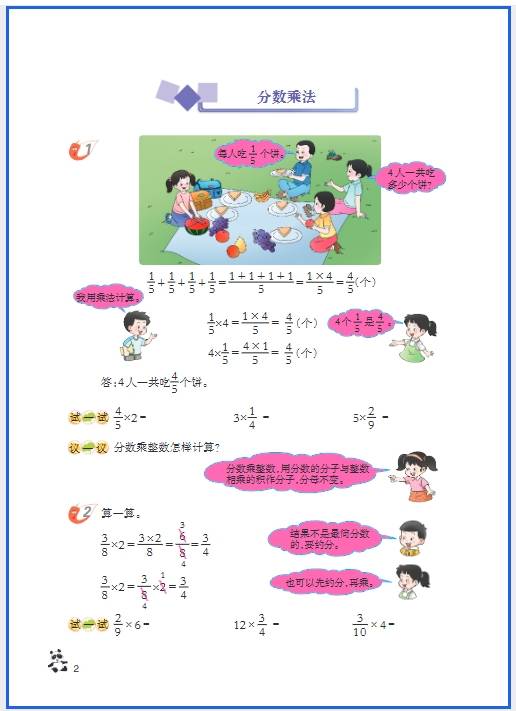
• 适用场景：简单整数、小数加减法（如 3.2+1.5）、表内乘法衍生的分数运算（如\(\frac{1}{3}×6\)）。
• 答题规范：结果写在 “=” 后，数字清晰，避免涂改（如\(0.8×0.5=0.4\)，不可写成\(.4\)）。
• 技巧：口算前默念算理（如小数乘法 “先算整数积，再点小数点”），复杂题可在草稿纸快速验算（如\(12.5÷0.5\)，想 “12.5×2=25”）。

1. 笔算题：分步书写，突出 “数位对齐、符号明确”

• 适用场景：小数四则混合运算、异分母分数加减法、整数乘除法（含因数倍数相关计算）。
• 答题规范：
• 小数运算：必须对齐小数点（加减法）或标注积 / 商的小数点位置（乘除法）。

例：\(3.6×2.5\)的笔算过程需写出：

3.6 （1位小数）

× 2.5 （1位小数）

------

180

72

------

9.00 （共2位小数，化简为9.0或9）

• 分数运算：异分母加减需写出 “通分” 步骤，结果要化简（除非题目要求不化简）。

例：\(\frac{1}{2}+\frac{1}{3}\)需写成：

$\frac{1}{2}+\frac{1}{3}=\frac{3}{6}+\frac{2}{6}=\frac{5}{6}$

• 混合运算：严格按 “先乘除后加减，有括号先算括号内” 的顺序，每步只算一个运算。

例：\(10-2.5×3\)需分步写：

10-2.5×3

=10-7.5

=2.5

• 禁忌：跳步计算（如直接写\(10-2.5×3=2.5\)）、符号遗漏（如漏写 “+”“×”）。

1. 脱式计算：“递等式书写，步骤清晰”

• 适用场景：含多个运算的混合式题（如\(（4.8+1.2）÷0.5×2\)）。
• 答题规范：等号对齐写在左侧，每步运算结果写在等号后，未参与运算的部分照抄。

例：

（4.8+1.2）÷0.5×2

=6÷0.5×2

=12×2

=24

（二）填空题：“精准对应，简洁规范”

填空题侧重 “概念理解、结果精准”，占分约 20%-25%，答题关键是 “紧扣题意、单位匹配、格式正确”。

1. 答题规范：

• 直接填写最终结果，数字、符号、单位需完整（如 “3.2 千克” 不可只写 “3.2”）。
• 分数结果需写最简形式（如填\(\frac{2}{4}\)不得分，需填\(\frac{1}{2}\)）。
• 小数结果按题目要求保留位数（如 “保留一位小数”，\(2.34\)需填\(2.3\)）。

1. 典型示例：

• 概念类：“\(\frac{3}{5}\)的分数单位是___”，需填 “\(\frac{1}{5}\)”（不可漏写分母）。
• 计算类：“一个平行四边形底 5cm，高 4cm，面积是___”，需填 “20cm²”（单位必带）。
• 应用类：“把 3 米长的绳子平均分成 4 段，每段长___米”，需填 “\(\frac{3}{4}\)”（不可填小数 0.75，除非题目允许）。

（三）选择题：“紧扣选项，标记依据”

选择题考查 “知识辨析、排除能力”，占分约 10%-15%，答题关键是 “圈画关键词、排除错项、验证对项”。

1. 答题规范：

• 用 “√” 或 “序号” 标记答案（按题目要求，如 “填 A/B/C/D” 或 “填序号①②③④”）。
• 草稿纸辅助：复杂题（如几何面积、概率）可画图或计算验证（如 “下列分数中最大的是（ ）”，可通分后比较）。

1. 技巧：“排除法 + 代入法”

• 排除法：先排除明显错误的选项（如 “2 的倍数个位是（ ）”，排除 “1、3、5” 等选项）。
• 代入法：将选项代入题干验证（如 “方程 3x+2=11 的解是（ ）”，代入 x=3 得 3×3+2=11，确认正确）。

（四）判断题：“找反例，明依据”

判断题侧重 “概念严谨性”，占分约 5%-10%，答题关键是 “紧扣定义、找反例推翻、标注理由（草稿纸）”。

1. 答题规范：

• 用 “√”“×” 标记，不可写 “对”“错”（除非题目允许），符号清晰不涂改。

1. 核心技巧：

• 正确题：紧扣教材定义（如 “小数的末尾添上 0，大小不变”，符合小数性质，打√）。
• 错误题：找 “反例” 或 “关键词错误”（如 “所有质数都是奇数”，反例 “2 是质数但不是奇数”，打 ×）。
• 易错点：注意 “一定”“可能”“所有” 等绝对化词语（如 “三角形面积一定比平行四边形小”，×，因未限定底和高）。

（五）应用题：“分步建模，逻辑闭环”

应用题是综合题型，占分约 25%-30%，核心考查 “建模能力”，答题关键是 “审题→建模→计算→检验→作答” 五步闭环。

1. 答题规范（核心步骤）：

• 第一步：审题圈画。用铅笔圈出 “关键词”（如 “平均”“一共”“比…… 多”“几分之几”）和 “数据 + 单位”（如 “5.8 元 / 千克”“3 米”）。
• 第二步：设未知数（方程题必备）。明确写 “解：设…… 为 x（单位）”（如 “解：设每千克苹果 x 元”）。
• 第三步：列算式 / 方程。
• 算术法：写出 “数量关系→算式”（如 “总价 ÷ 数量 = 单价”，再列\(29÷5=5.8\)）。
• 方程法：根据等量关系列方程（如 “买 3 千克苹果和 2 千克梨共花 20 元，梨每千克 4 元，求苹果单价”，列\(3x+2×4=20\)）。
• 第四步：计算与单位。分步计算，每步带单位（如 “3x=20-8=12，x=12÷3=4（元）”）。
• 第五步：检验与作答。
• 检验：代入结果验证（如 x=4，3×4+2×4=20，符合题意）；实际问题需检验 “合理性”（如 “人数”“数量” 不可为负数或小数）。
• 作答：用 “答：……” 收尾，语句完整（如 “答：每千克苹果 4 元”）。

1. 典型示例（分数应用题）：

题目：一袋大米 20 千克，吃了\(\frac{3}{4}\)，还剩多少千克？

答题过程：

第一步：圈画“20千克”“吃了$\frac{3}{4}$”“还剩”。

第二步：数量关系：剩下的重量=总重量-吃了的重量。

第三步：计算吃了的重量：20×$\frac{3}{4}$=15（千克）。

第四步：剩下的重量：20-15=5（千克）。

第五步：检验：15+5=20（千克），符合总重量；答：还剩5千克。

二、通用答题规范与高分技巧

（一）基础规范：避免 “会做但扣分”

1. 书写要求：数字、符号、字母书写清晰（如 “0” 不可写成 “6”，“x” 不可写成 “×”）；分数的分子分母对齐，分数线平直。
2. 单位规范：计算结果带单位（应用题必带，填空题看题干是否给单位）；单位换算统一（如 “1 米 5 分米” 换算成 “1.5 米” 再计算）。
3. 修改规范：错误处用 “横线划掉” 后重写，不可涂改、擦除（如\(3.2+1.8=5.0\)，错写成\(4.0\)，应划掉\(4.0\)再写\(5.0\)）。

（二）高分技巧：针对性提分

1. 草稿纸使用：按 “题号顺序” 分区书写，步骤清晰（如 “计算题 1”“应用题 2”），方便检查时追溯思路。
2. 时间分配：选择题、填空题控制在 15-20 分钟，计算题 20-25 分钟，应用题 30-35 分钟，预留 5-10 分钟检查。
3. 检查重点：

• 计算题：重查 “小数点位置”“通分是否正确”“混合运算顺序”。
• 应用题：重查 “等量关系”“单位是否统一”“结果是否合理”。
• 填空题：重查 “分数是否最简”“单位是否遗漏”。

三、易错点规避指南

1. 计算类易错点：

• 小数除法：除数是小数时未转化为整数（如\(1.8÷0.3\)，错算成\(1.8÷3=0.6\)，正确应为\(18÷3=6\)）。
• 分数减法：异分母分数直接减（如\(\frac{1}{2}-\frac{1}{3}\)，错算成\(\frac{0}{1}\)，正确应为\(\frac{3}{6}-\frac{2}{6}=\frac{1}{6}\)）。

1. 应用类易错点：

• 漏看条件：如 “打折问题” 漏看 “八折” 即 “原价 ×0.8”，错算成 “原价 ×8”。
• 单位混淆：如 “面积单位” 与 “长度单位” 混用（求面积错写 “cm”，应写 “cm²”）。

1. 概念类易错点：

• 质数与合数：错把 “1” 归为质数（1 既不是质数也不是合数）。
• 方程定义：错把 “3x+2” 叫方程（方程需含 “=” 且有未知数）。