2025秋新教材北京版小学三年级数学(上册)电子课本高清PDF版可打印
2025年学生将迎来新版教材,新教材将更加重视思维和阅读!为了方便广大学生在暑假预习新学期的课本知识,我们整理了2025新北京版三年级数学(上册)一电子课本,以图片的形式呈现给大家,希望对同学们的暑期学习有所帮助。
以下是部分内容截图,完整信息请查看 PDF 文件




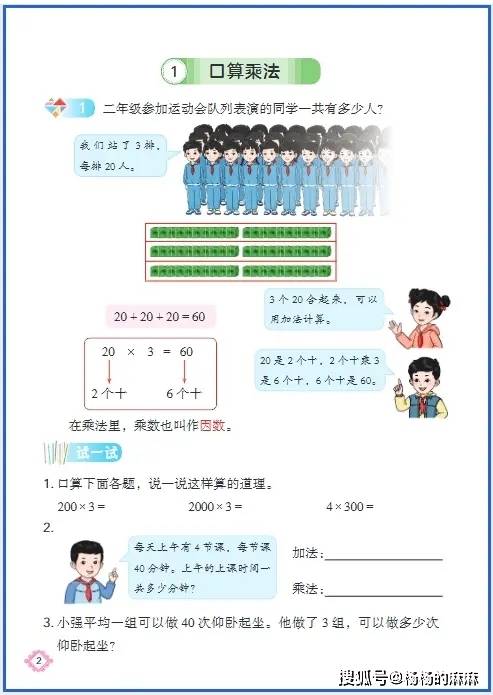

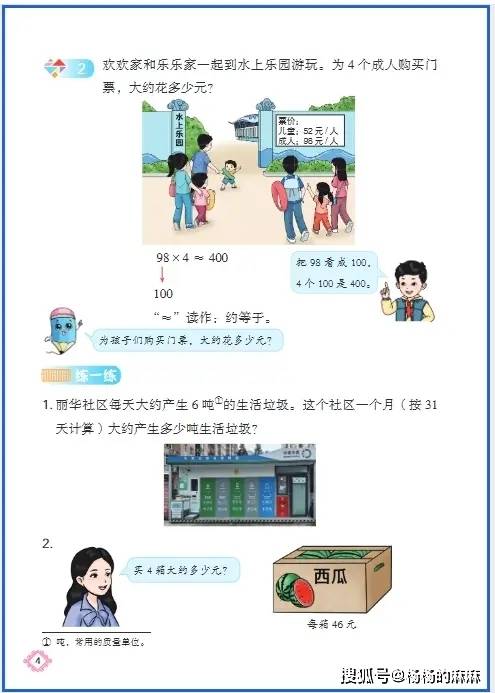
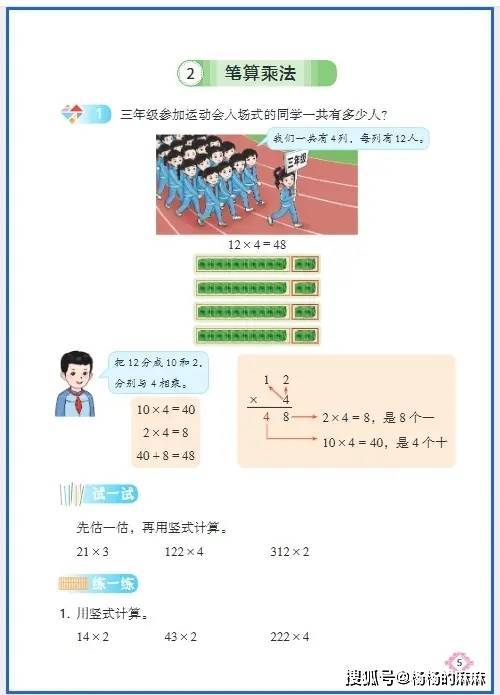

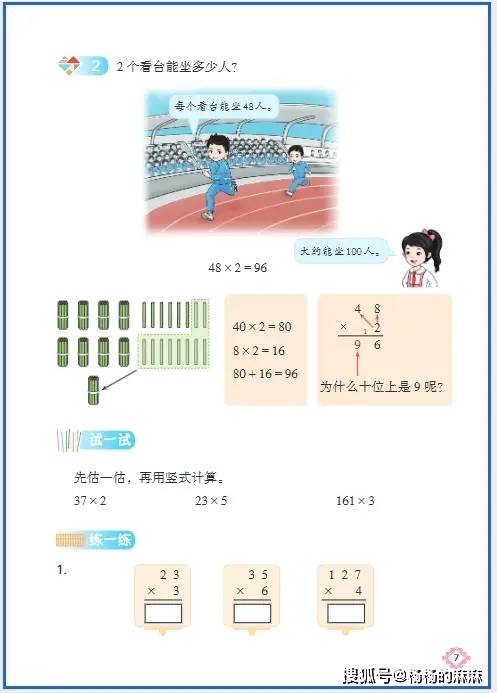




用 “生活实例” 搭桥:让数学概念从 “记不住” 到 “用得活”
很多人学数学概念时,总困在 “背定义、套公式” 里,遇到变式题就卡壳 —— 其实问题出在 “没把抽象符号和实际场景挂钩”。真正的概念学习,是用实例当 “翻译官”,把冰冷的逻辑转化为可感知、能应用的知识。以下按 “概念解构逻辑 — 分学段新例 — 实操技巧 — 避坑指南” 展开,教你用实例吃透数学概念。
一、概念解构的 “三维锚点”:实例要精准对接核心
找实例不是 “随便举个例子”,而是要瞄准概念的三个核心维度,才能避免 “浮于表面”:
- 本质锚点:用实例说清 “概念到底是什么”(排除非本质特征干扰);
- 逻辑锚点:用实例讲透 “为什么需要这个概念”(解决什么现实问题);
- 应用锚点:用实例展示 “怎么用这个概念解决新问题”(关联具体场景)。
二、分学段新例:从 “日常感知” 到 “模型应用”
不同学段的数学概念难度不同,实例选择要贴合认知水平 —— 小学重 “生活场景”,初中重 “直观模型”,高中重 “问题建模”。
(一)小学数学:用 “日常小事” 解锁具象概念
小学数学概念多与 “衣食住行” 相关,实例优先选 “可触摸、可操作” 的场景,帮孩子建立 “概念 = 生活工具” 的认知。
例 1:概念 —— 百分数的 “实际意义”(六年级)
死记定义:表示一个数是另一个数的百分之几的数,叫百分数(也叫百分率或百分比)。
(易混淆点:百分数是 “比例关系”,不是 “具体量”,不带单位)
用实例拆解:
- 本质锚点(是什么):
实例 1(折扣):商场 “八折促销”,即 “现价是原价的 80%”—— 比如原价 100 元的衣服,现价 = 100×80%=80 元(这里 80% 是 “现价与原价的比例”,不是 80 元);
实例 2(增长率):班级上次考试及格 30 人,这次及格 36 人,“及格率增长了 20%”—— 增长的比例是(36-30)÷30=20%,不是 “增长 20 人”。
作用:通过 “折扣 vs 增长率”,明确百分数是 “两个数的比例”,而非具体数量。
- 逻辑锚点(为什么):
反例:若用分数表示折扣(如 “4/5 折”),不如 “80%” 直观;比较 “甲班及格率 90%” 和 “乙班及格率 85%”,比比较 “9/10 和 17/20” 更快捷 —— 说明百分数是 “为了简化比例比较” 而产生的。
- 应用锚点(怎么用):
问题:妈妈买了一桶 5 升的食用油,第一个月用了 20%,第二个月用了剩下的 30%,还剩多少升?
计算:第一个月剩余 = 5×(1-20%)=4 升;第二个月剩余 = 4×(1-30%)=2.8 升 —— 用百分数解决 “逐步消耗” 的实际问题。
例 2:概念 —— 长方体的 “体积公式”(五年级)
死记公式:长方体体积 = 长 × 宽 × 高(V=a×b×h)。
(易混淆点:体积是 “空间大小”,不是 “表面积” 或 “棱长总和”)
用实例拆解:
- 本质锚点:用 “快递盒装小正方体” 理解 —— 一个长 3cm、宽 2cm、高 2cm 的盒子,每行能摆 3 个 1cm³ 的小正方体,摆 2 行(宽),叠 2 层(高),总个数 = 3×2×2=12 个,即体积 12cm³(体积本质是 “单位体积的个数”);
- 逻辑锚点:为什么需要体积公式?比如快递站打包,要知道箱子能装多少件小商品(需算体积),比 “一个一个摆小正方体” 更高效;
- 应用锚点:问题:一个长方体收纳箱,长 50cm、宽 40cm、高 30cm,能装下多少个棱长 10cm 的正方体玩具?
计算:收纳箱体积 = 50×40×30=60000cm³;单个玩具体积 = 10×10×10=1000cm³;个数 = 60000÷1000=60 个。
(二)初中数学:用 “直观模型” 拆解抽象关系
初中数学开始涉及 “符号化”“逻辑推理”,实例可借助 “图形、表格、实际问题模型”,帮你从 “具象” 过渡到 “抽象”。
例 1:概念 —— 二元一次方程组(七年级)
死记定义:含有两个未知数,并且含有未知数的项的次数都是 1 的整式方程组。
(易混淆点:“两个未知数”“次数 1”“整式”,缺一不可)
用实例拆解:
- 本质锚点(是什么):
实例:买 2 支钢笔和 3 本笔记本共花 34 元,买 1 支钢笔和 2 本笔记本共花 19 元,求钢笔和笔记本的单价。
设钢笔单价 x 元,笔记本单价 y 元,列方程组:{2x+3y=34x+2y=19
这里 x、y 是两个未知数,每项次数都是 1,符合 “二元一次方程组” 定义。
- 逻辑锚点(为什么):
若用算术法:先算 “1 支钢笔 + 1 本笔记本”=34-19=15 元,再算 “1 本笔记本”=19-15=4 元,过程绕且易错;用方程组 “直接翻译题干关系”,更清晰 —— 说明方程组是 “解决多未知数问题” 的工具。
- 应用锚点(怎么用):
解方程组:由第二个方程得 x=19-2y,代入第一个方程:2 (19-2y)+3y=34→38-4y+3y=34→y=4,再得 x=11—— 即钢笔 11 元,笔记本 4 元。
例 2:概念 —— 全等三角形的 “判定定理(SAS)”(八年级)
死记定理:两边及其夹角分别相等的两个三角形全等(SAS)。
(易混淆点:“夹角” 是关键,不是 “任意角”)
用实例拆解:
- 本质锚点(是什么):
实例:配钥匙时,要保证新钥匙和原钥匙 “对应边长度相等、对应夹角相等”—— 比如原钥匙某部分 “两边长 2cm、3cm,夹角 60°”,新钥匙同样按这个规格制作,才能和锁芯匹配(对应三角形 “两边及夹角相等,形状大小完全相同”)。
- 逻辑锚点(为什么):
反例:若只保证 “两边相等,非夹角相等”(如两边 2cm、3cm,夹角换成 90°),新钥匙会比原钥匙 “宽”,无法插入锁芯 —— 说明 “夹角” 是确保 “全等” 的核心,缺了就不能保证形状大小一致。
- 应用锚点(怎么用):
问题:已知 AB=AD,∠BAC=∠DAC,AC=AC,求证△ABC≌△ADC。
证明:∵AB=AD(已知),∠BAC=∠DAC(已知),AC=AC(公共边),∴△ABC≌△ADC(SAS)—— 用定理解决几何证明题。
(三)高中数学:用 “问题建模” 理解抽象模型
高中数学概念更侧重 “抽象逻辑”“模型应用”,实例要 “从具体问题提炼模型,再用模型反推概念本质”。
例 1:概念 —— 三角函数的 “周期性”(高一)
死记定义:对于函数 f (x),如果存在一个非零常数 T,使得当 x 取定义域内的每一个值时,都有 f (x+T)=f (x),那么函数 f (x) 就叫做周期函数,T 叫做这个函数的周期。
(易混淆点:“每一个值”“非零常数 T”,周期是 “最小正周期”)
用实例拆解:
- 本质锚点(是什么):
实例 1(钟表):钟表指针每 12 小时转一圈(时针),每 60 分钟转一圈(分针)—— 比如时针指向 3 点,12 小时后仍指向 3 点,即 “f (x+12)=f (x)”,12 是时针的周期;
实例 2(四季):每年按 “春→夏→秋→冬” 循环,周期是 12 个月 —— 今年 3 月是春季,明年 3 月还是春季,符合 “f (x+12)=f (x)”。
- 逻辑锚点(为什么):
为什么需要 “周期性”?比如预测明年的季节、计算钟表指针位置,不用 “从头开始算”,只需按周期重复规律即可 —— 说明周期性是 “描述重复变化现象” 的数学工具。
- 应用锚点(怎么用):
问题:已知 f (x)=sinx,求 f (π+2π) 的值。
解:∵sinx 的周期是 2π,∴f (π+2π)=f (π)=sinπ=0。
例 2:概念 —— 导数的 “几何意义”(高二)
死记定义:函数 y=f (x) 在点 x₀处的导数 f’(x₀),表示函数图像在点 P (x₀,f (x₀)) 处的切线斜率。
(易混淆点:导数是 “切线斜率”,不是 “切线方程” 或 “函数值”)
用实例拆解:
- 本质锚点(是什么):
实例:开车上山时,路面的 “坡度” 就是函数图像的 “导数”—— 比如某段山路对应的函数 y=0.5x,导数 f’(x)=0.5(切线斜率),表示 “每前进 1 公里,海拔上升 0.5 公里”(缓坡);若某段山路 y=2x,导数 f’(x)=2(陡坡),表示 “每前进 1 公里,海拔上升 2 公里”;下坡时 y=-x,导数 f’(x)=-1(负斜率),表示 “每前进 1 公里,海拔下降 1 公里”。
- 逻辑锚点(为什么):
为什么需要导数的几何意义?比如工程师设计山路,通过导数(坡度)判断车辆能否安全行驶 —— 坡度太大(导数绝对值大),车辆容易溜坡;坡度适中(导数绝对值小),更安全 —— 说明导数是 “量化变化快慢” 的工具。
- 应用锚点(怎么用):
问题:求函数 y=x² 在点 (2,4) 处的切线斜率。
解:∵y’=2x,∴在 x=2 处的导数 f’(2)=4,即切线斜率为 4。
三、实操技巧:自己 “造实例” 的 3 步心法
会自己设计实例,才是 “吃透概念” 的标志。按以下 3 步,轻松为任何概念找对实例:
步骤 1:“拆概念”—— 抓出定义里的 “关键词”
比如学 “菱形”,先拆关键词:①四边相等;②平行四边形(两组对边分别平行)。
步骤 2:“找场景”—— 匹配 “符合关键词” 的具体对象
- 生活场景:菱形的窗花(四边相等、对边平行)、菱形的风筝面(符合两个关键词);
- 数学场景:坐标系中,点 (0,0)、(1,2)、(3,1)、(2,-1) 连接成的图形(计算边长均为√5,对边平行)。
步骤 3:“验正反”—— 用实例 “验证” 或 “反驳” 概念
- 正例:菱形窗花符合 “四边相等 + 平行四边形”→ 是菱形;
- 反例:普通平行四边形(边长 2、3、2、3)—— 只满足 “平行四边形”,不满足 “四边相等”→ 不是菱形;等腰梯形(对边不平行)—— 不满足 “平行四边形”→ 不是菱形。
四、避坑指南:实例使用的 2 个 “禁忌”
禁忌 1:用 “特殊实例” 代替 “一般概念”
比如学 “反比例函数 y=k/x(k≠0)”,不能只举 “k=1(y=1/x,图像在一、三象限)”,还要举 “k=-2(y=-2/x,图像在二、四象限)”—— 避免误以为 “反比例函数图像只在正象限”;还要举 “k=3(y=3/x)”,说明 “k 不同,图像位置或陡峭程度不同”,覆盖概念的 “一般性”。
禁忌 2:“脱离概念核心” 的实例
比如解释 “无理数”,不能只说 “无限不循环小数就是无理数”,要举 “边长为 1 的正方形,对角线长度是√2(无限不循环)”—— 这个实例紧扣 “无理数的产生背景(几何测量)”,而非单纯重复定义;若举 “0.1010010001…”,虽也是无理数,但没关联概念的 “应用场景”,理解会更抽象。
总结:实例是概念的 “活灵魂”
用实例学数学概念,不是 “多此一举”,而是让抽象逻辑 “落地” 的关键 —— 先在生活里 “摸透” 概念的本质、逻辑和用途,再用它解决新问题,形成 “具体→抽象→具体” 的闭环。久而久之,你会发现:数学概念不再是 “背完就忘的符号”,而是能帮你解决实际问题的 “实用工具”—— 这正是数学思维的核心。
