2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025新人教版五年级数学（上册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

以下是部分内容截图，完整信息请查看 PDF 文件

一、数与代数：筑牢数学核心基础

作为五年级数学的 “根基模块”，数与代数在延续整数知识的同时，引入小数、分数的系统学习，重点培养学生对 “数的意义” 的深层理解与运算逻辑。

1. 小数的认识与运算：打通 “整数” 与 “小数” 的连接

• 意义理解：结合生活场景具象化小数，比如把 1 元平均分成 10 份，1 份是 0.1 元（1 角）；把 1 米平均分成 100 份，1 份是 0.01 米（1 厘米），让学生明白 “小数是分母为 10、100、1000…… 的特殊分数”。
• 读写与性质：读数时结合 “单位” 辅助理解（如 2.5 千克读作 “二点五千克”，突出小数与实际量的关联）；利用 “人民币兑换”（1.5 元 = 1.50 元）、“长度测量”（3.0 米 = 3 米）等例子，验证小数末尾添 0 / 去 0 大小不变的性质，同时强调 “中间的 0 不能随意删改”（如 3.05≠3.5）。
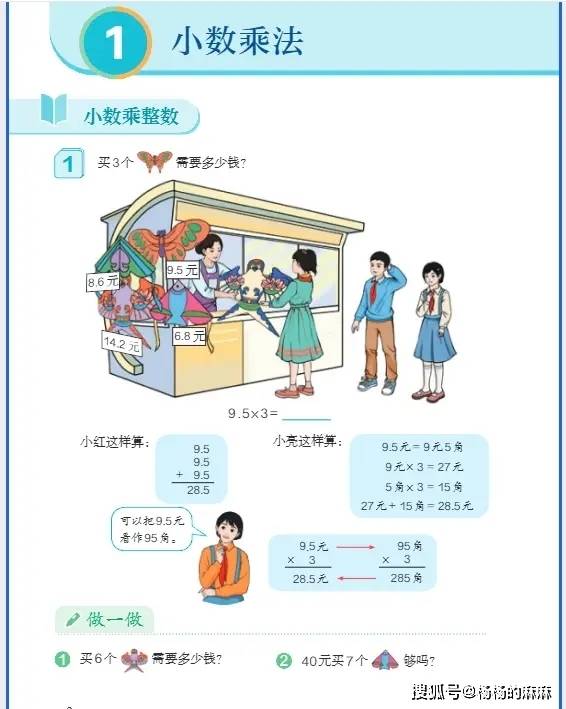
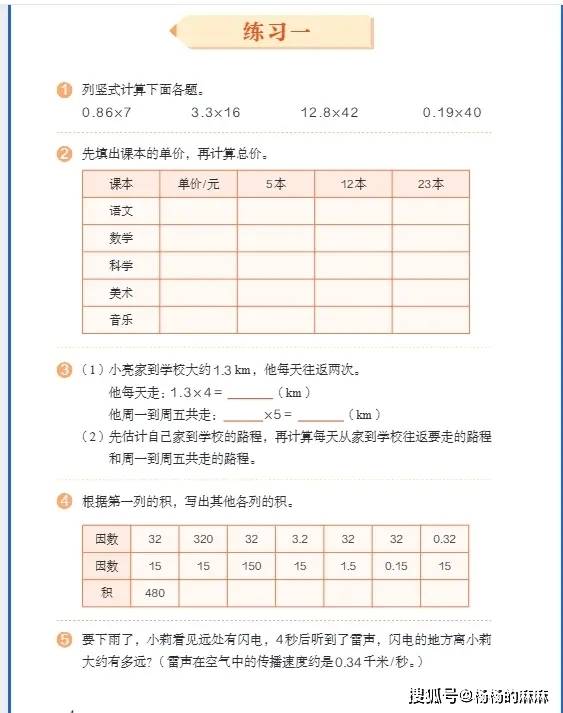
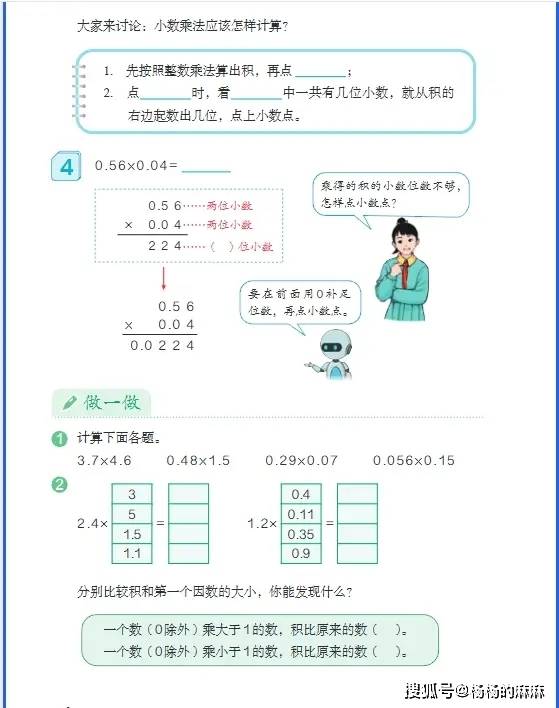
• 四则运算：加减法聚焦 “相同计数单位对齐”，用 “元角分计算”（3 元 2 角 + 5 角 8 分 = 3.2 元 + 0.58 元 = 3.78 元）帮助学生理解 “小数点对齐” 的本质；乘除法结合 “购物计价”（买 2.5 千克苹果，每千克 8.4 元，总价 = 2.5×8.4）、“单位换算”（5.6 米 ÷0.7=8 米）等场景，降低运算抽象感，同时提醒 “积的小数位数确定”“除数变整数时被除数同步扩大” 的关键步骤。

2. 分数的初步认识（下册重点）：建立 “部分与整体” 的认知

• 意义与单位：用 “分物品” 的例子引入，比如把 6 块蛋糕平均分成 3 份，1 份是 2 块，也可以表示为整体的 1/3；把 1 块蛋糕平均分成 4 份，1 份是 1/4（分数单位），3 份就是 3 个 1/4（3/4），明确 “分子数份数，分母表平均分的总份数”。
• 分类与关系：通过对比 “蛋糕分配” 场景区分分数类型 —— 把 1 块蛋糕平均分成 2 份，取 1 份是真分数（1/2）；把 3 块蛋糕平均分成 2 份，取 2 份是假分数（2/2），取 3 份是带分数（1 又 1/2）；用 “分绳子”（3 米长的绳子平均分成 5 段，每段长 3÷5=3/5 米）直观呈现分数与除法的对应关系。
• 基本性质：借助 “折纸实验”，把一张正方形纸对折 2 次得到 1/4，对折 3 次得到 2/8，对比发现 1/4=2/8；再对折 4 次得到 4/16，验证 1/4=2/8=4/16，让学生在动手操作中理解 “分子分母同乘 / 除以非 0 数，分数大小不变”，为后续约分、通分铺垫。

3. 整数的拓展与运算：深化 “数的关联” 认知

• 因数与倍数：以 “拼长方形” 为载体，用 12 个小正方形拼长方形，能拼成 1×12、2×6、3×4 三种形式，对应得出 12 的因数有 1、2、3、4、6、12，12 是 1、2、3、4、6、12 的倍数，让抽象概念具象化。
• 倍数特征与质数合数：用 “百数表圈数” 游戏，圈出 2 的倍数（个位 0、2、4、6、8）、5 的倍数（个位 0、5）、3 的倍数（各位和是 3 的倍数），通过观察总结规律；再通过 “找因数个数” 区分质数（如 2、3、5，只有 2 个因数）、合数（如 4、6、8，有 3 个及以上因数），明确 1 既不是质数也不是合数。
• 最大公因数与最小公倍数：用 “铺地砖” 问题引入，比如用边长几分米的正方形地砖能正好铺满长 12 分米、宽 18 分米的长方形，引导学生找 12 和 18 的公因数，其中最大的 6 就是最大公因数；用 “找共同休息日” 问题（甲每 3 天休息一次，乙每 4 天休息一次，下次共同休息是第几天），引导学生找 3 和 4 的公倍数，其中最小的 12 就是最小公倍数，同时介绍短除法的便捷计算方法。

二、图形与几何：发展空间想象能力

该模块聚焦 “平面图形面积” 与 “立体图形特征”，通过 “推导过程可视化”“动手操作体验”，帮助学生建立空间观念，掌握图形计算逻辑。

1. 平面图形的面积：理解 “转化思想” 的核心

• 平行四边形：用 “剪拼法” 演示 —— 把平行四边形沿高剪开，平移拼成一个长方形，观察发现 “长方形的长 = 平行四边形的底，长方形的宽 = 平行四边形的高”，由此推导面积公式 S=ah；课后让学生用硬纸板制作平行四边形，动手剪拼验证，加深对转化过程的理解。
• 三角形与梯形：三角形面积推导采用 “拼组法”，用两个完全相同的三角形拼成一个平行四边形，得出 “三角形面积 = 平行四边形面积 ÷2=ah÷2”；梯形则用两个完全相同的梯形拼成平行四边形，发现 “平行四边形的底 = 梯形上底 + 下底，高 = 梯形的高”，推导公式 S=(a+b) h÷2；可让学生用三角板、梯形卡片分组拼组，记录推导过程。
• 组合图形：结合 “房屋平面图计算面积”“不规则草坪面积估算” 等实际场景，教学生用 “分割法”（把组合图形分成长方形、三角形等基本图形）或 “添补法”（把图形补成正方形、长方形，再减去多余部分）计算；通过 “设计专属图形” 活动，让学生自主创作组合图形并计算面积，提升应用能力。

2. 长方体与正方体：构建 “立体图形” 认知体系

• 特征对比：用牙膏盒（长方体）、魔方（正方体）实物观察，记录两者的面、棱、顶点特征 —— 长方体 6 个面中相对面完全相同，12 条棱分 3 组（长、宽、高）且每组长度相等；正方体 6 个面都是正方形且完全相同，12 条棱长度全相等，明确 “正方体是特殊的长方体”。
• 棱长总和与表面积：结合 “包装礼物” 场景，计算长方体礼盒的棱长总和（确定彩带长度）、表面积（确定包装纸大小），推导公式：长方体棱长总和 = 4×(长 + 宽 + 高)，表面积 = 2×(长 × 宽 + 长 × 高 + 宽 × 高)；正方体棱长总和 = 12× 棱长，表面积 = 6× 棱长 × 棱长，同时提醒 “表面积计算需结合实际，如无盖鱼缸只需算 5 个面”。
• 体积与单位：用 “摆小正方体” 实验推导体积公式 —— 长方体盒子里摆 1cm³ 的小正方体，长摆 5 个、宽摆 3 个、高摆 2 个，共摆 5×3×2=30 个，体积就是 30cm³，得出 V = 长 × 宽 × 高；正方体同理推导 V = 棱长 × 棱长 × 棱长，再统一为 V = 底面积 × 高（Sh）；通过 “单位换算游戏”（1dm³=1L，1cm³=1mL，用量杯、正方体容器直观感受），掌握体积单位间的进率。

三、应用题与统计：提升综合运用能力

该模块侧重 “知识联系实际”，通过典型应用题梳理解题思路，借助统计图表培养数据分析能力，是数学 “学以致用” 的关键。

1. 典型应用题：掌握 “解题逻辑” 与 “场景适配”

• 小数与分数应用题：小数应用题结合 “购物计算”（买 3.5 千克香蕉，每千克 5.8 元，带 20 元够吗？先算 3.5×5.8=20.3 元，再比较 20.3＞20，得出不够）、“单位换算”（1 吨煤 425.5 元，买 0.8 吨需多少元）；分数应用题聚焦 “部分与整体关系”，如 “一袋大米 25 千克，吃了 3/5，吃了多少千克？”（25×3/5=15 千克）、“小明有 12 支笔，小红有 8 支，小红的笔是小明的几分之几？”（8÷12=2/3），解题时先明确 “单位 1”，再判断用乘法还是除法。
• 行程与工程问题：行程问题用 “线段图” 辅助分析，如 “甲、乙两车分别从 A、B 两地同时出发，相向而行，甲每小时行 60 千米，乙每小时行 80 千米，3 小时后相遇，A、B 两地相距多少千米？”，线段图中标出速度、时间，直观呈现 “总路程 = 速度和 × 相遇时间”；工程问题常把 “工作总量看作 1”，如 “一项工程，甲单独做 8 天完成，乙单独做 10 天完成，两人合作几天完成？”，先算效率和（1/8+1/10=9/40），再用 1÷9/40=40/9 天，培养 “总量归一” 的解题思维。

2. 统计与可能性：培养 “数据意识” 与 “概率认知”

• 统计图：结合 “班级身高统计” 绘制条形统计图，直观比较不同身高段的人数多少；结合 “一周气温变化” 绘制折线统计图，观察气温升降趋势，学会计算平均数（如一周平均气温 = 总气温 ÷7）、中位数（按顺序排列后中间的数），分析数据背后的信息（如 “身高 140-145 厘米的人数最多，需重点关注该身高段学生的健康情况”）。
• 可能性：通过 “摸球实验”（盒子里放 5 个红球、2 个白球，摸出红球可能性大）、“抛硬币”（正面朝上和反面朝上可能性相等）等活动，用 “一定”“可能”“不可能” 描述事件（如 “太阳不可能从西边升起”“明天可能下雨”），理解 “可能性大小与数量多少相关”，培养初步的概率思维。

四、重点难点突破与学习方法：高效避坑与能力提升

针对五年级数学的易错点，结合学生认知特点，提供具象化、实用性强的学习策略。

1. 易错点辨析：精准避开 “认知陷阱”

• 小数运算：重点关注 “小数点对齐”，如计算 3.6+2.05 时，易误写成 3.6+2.05=5.65（正确应为 5.65？不，正确是 3.60+2.05=5.65，此处需注意补 0），可在草稿纸上标注数位，确保相同计数单位相加；小数除法中，除数是小数时易漏扩倍，如 0.36÷0.04，需先把除数变成 4，被除数同步扩到 36，再算 36÷4=9。
• 面积与体积：区分 “面积是平面大小，体积是空间大小”，如 “一个正方体棱长 6 厘米，求表面积和体积”，表面积 = 6×6×6=216 平方厘米，体积 = 6×6×6=216 立方厘米，数值相同但单位不同，不能比较；避免混淆公式，如长方体表面积易漏算 “相对面”，体积易误将 “棱长和” 代入公式。
• 分数与除法：牢记 “分母不能为 0”，如 a÷b=a/b 中 b≠0；假分数与带分数转化时，易出现 “商与分母相乘错误”，如 7/3 转化为带分数，7÷3=2 余 1，应为 2 又 1/3，而非 2 又 3/1。

2. 实用学习法：让抽象知识 “看得见、摸得着”

• 具象化理解：用生活实物辅助学习，如用积木拼搭长方体、正方体，理解棱长、表面积、体积的关系；用折纸、剪图形的方式，推导平行四边形、三角形的面积公式；用分数卡片（如 1/2、1/3、2/3）拼接，理解分数加减法的算理。
• 错题整理与生活联系：按 “计算错误”“思路错误”“单位错误” 分类整理错题，标注错误原因（如 “小数乘法中积的小数位数数错”），定期复习；把数学知识融入生活，如购物时算总价、分蛋糕时用分数、整理房间时测量家具尺寸算占地面积，让抽象知识在实践中内化。