如需全套各科电子课本PDF版（可下载打印）

请关注公众号“禾沐教辅网”（ ID: hemujiaofu ）

关注后自动获取资料合集（包含下列推荐资料）

500T学习资料分享

同步25年秋季学校教学进度持续更新.......

鲁教版九年级上册数学电子课本的目录如下：

第一章 反比例函数

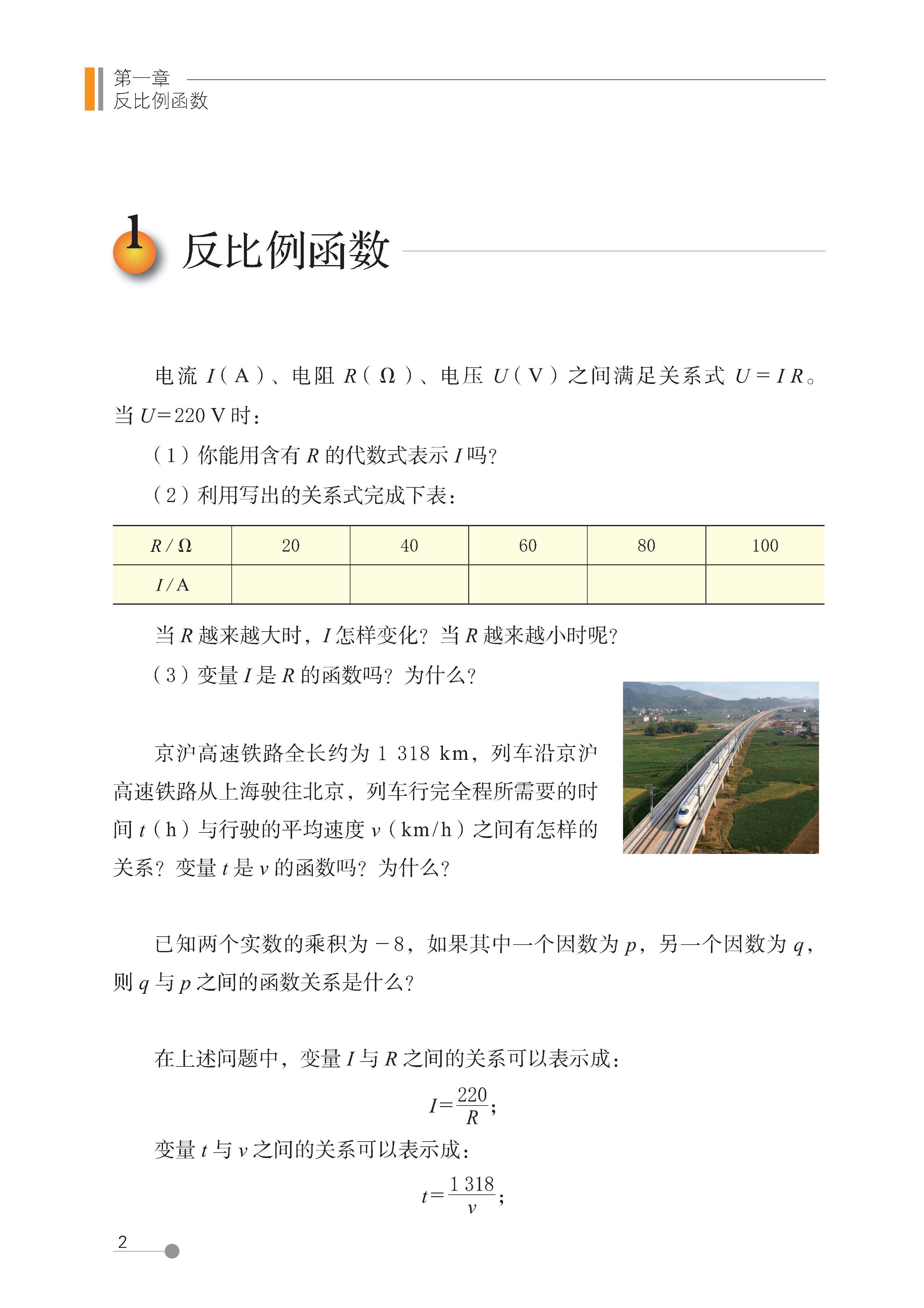
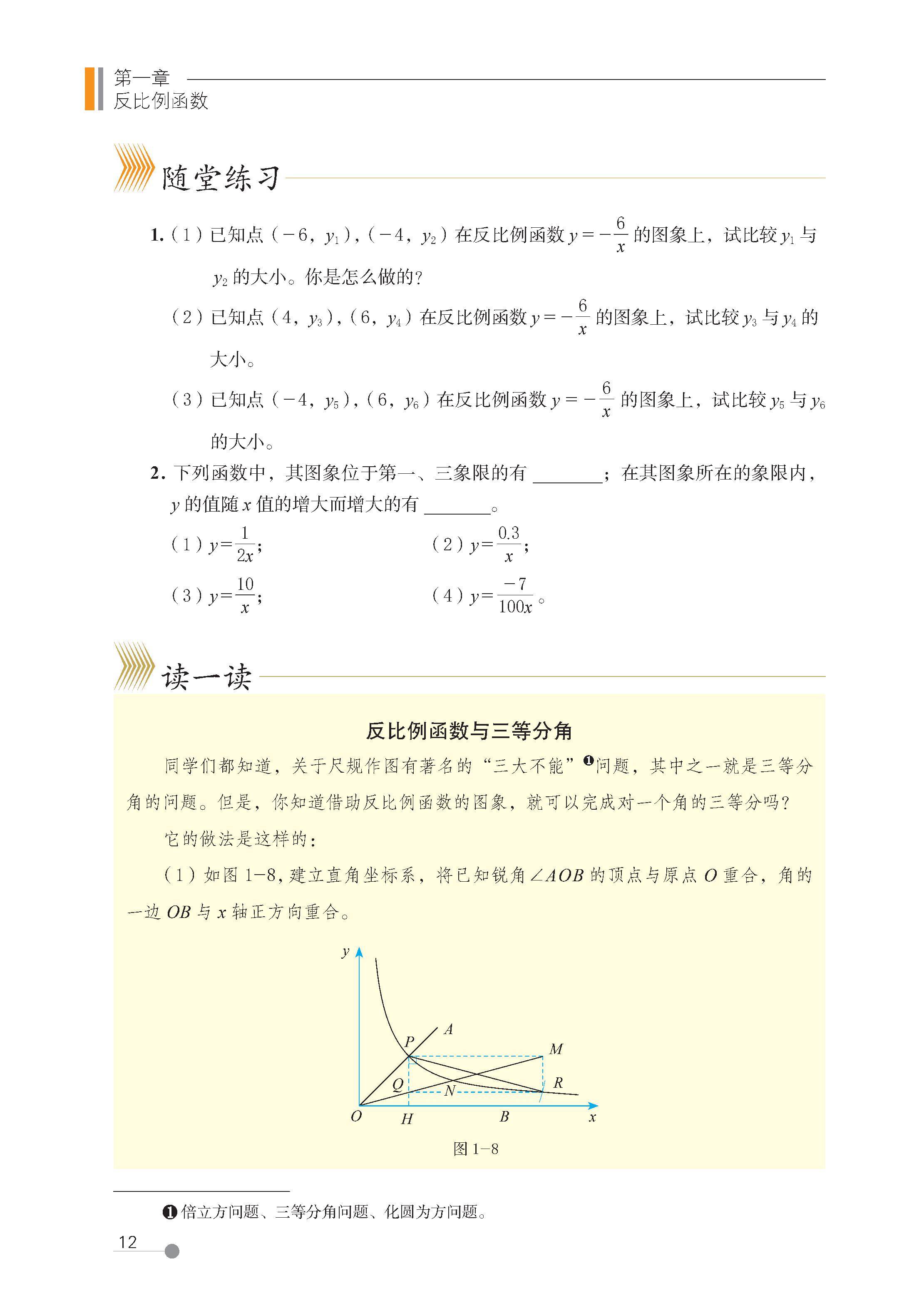
1 反比例函数

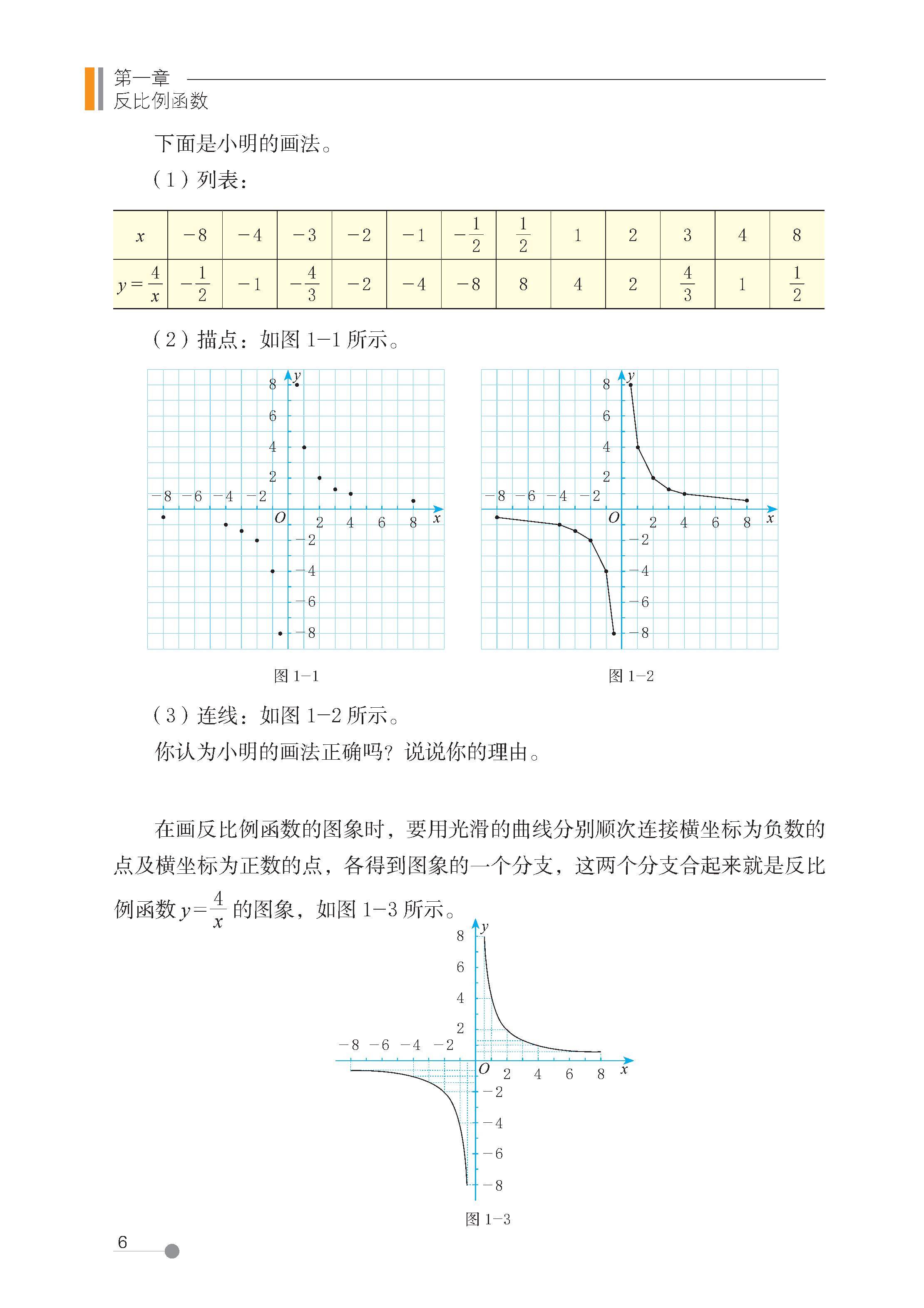
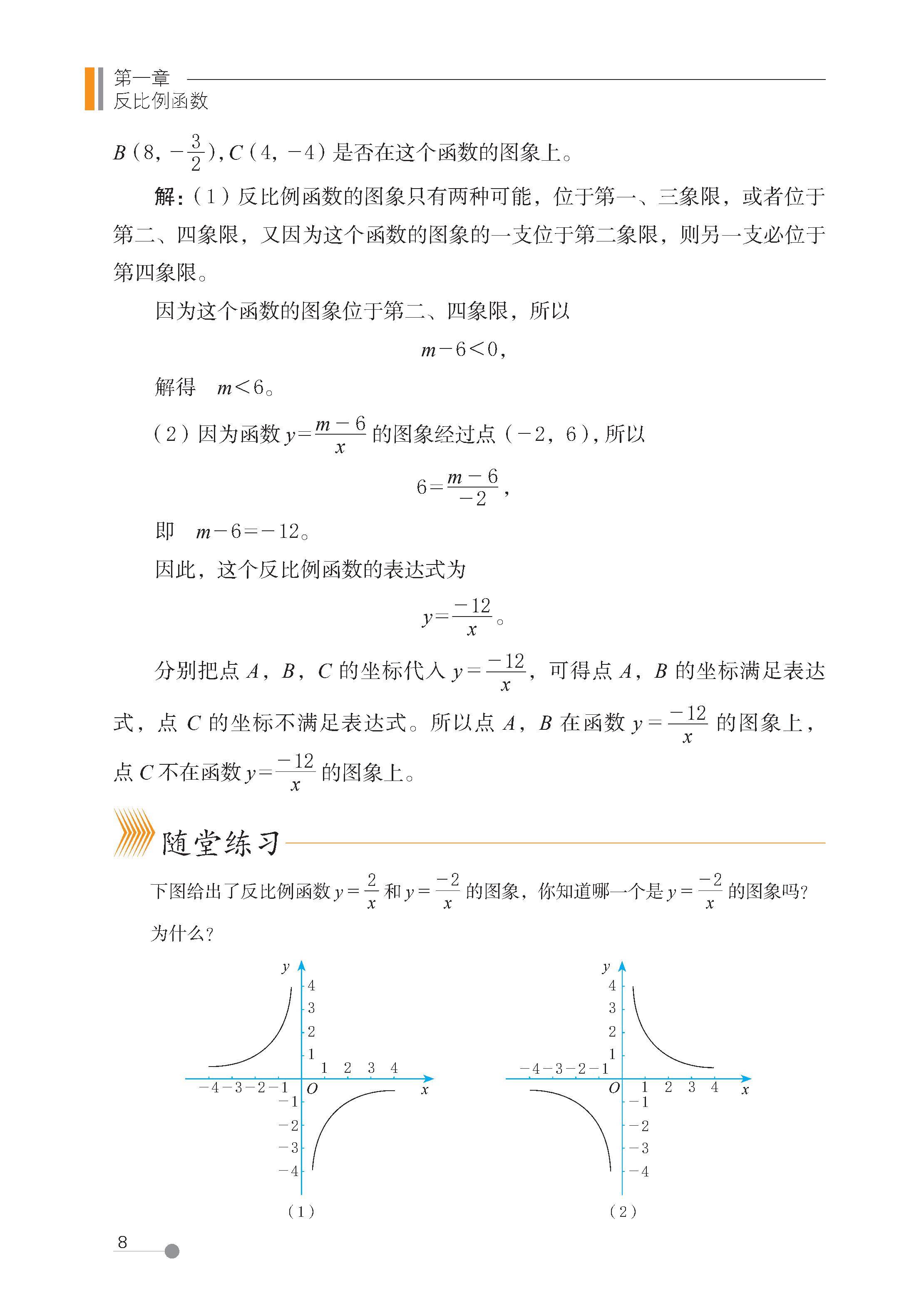
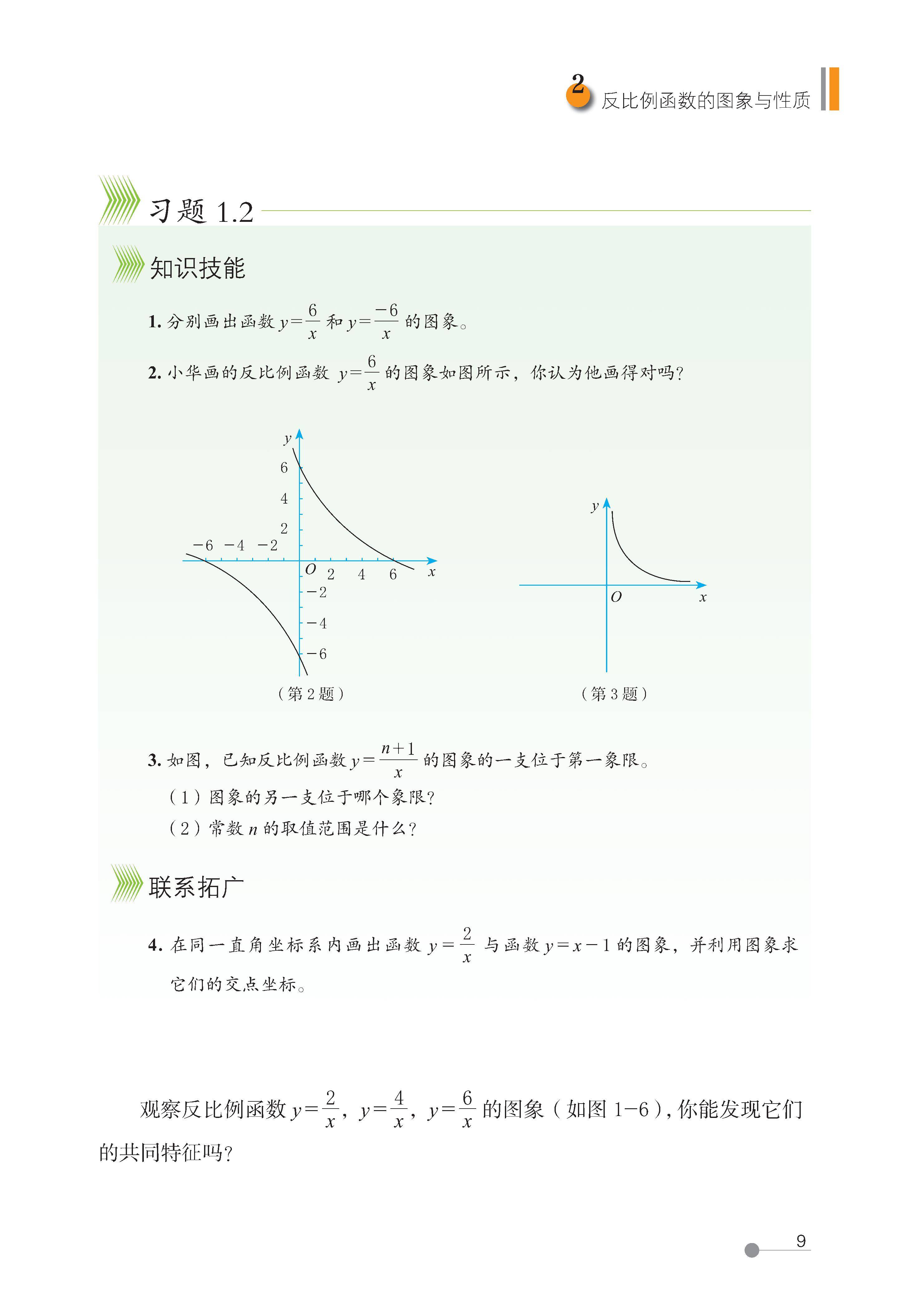
2 反比例函数的图像与性质

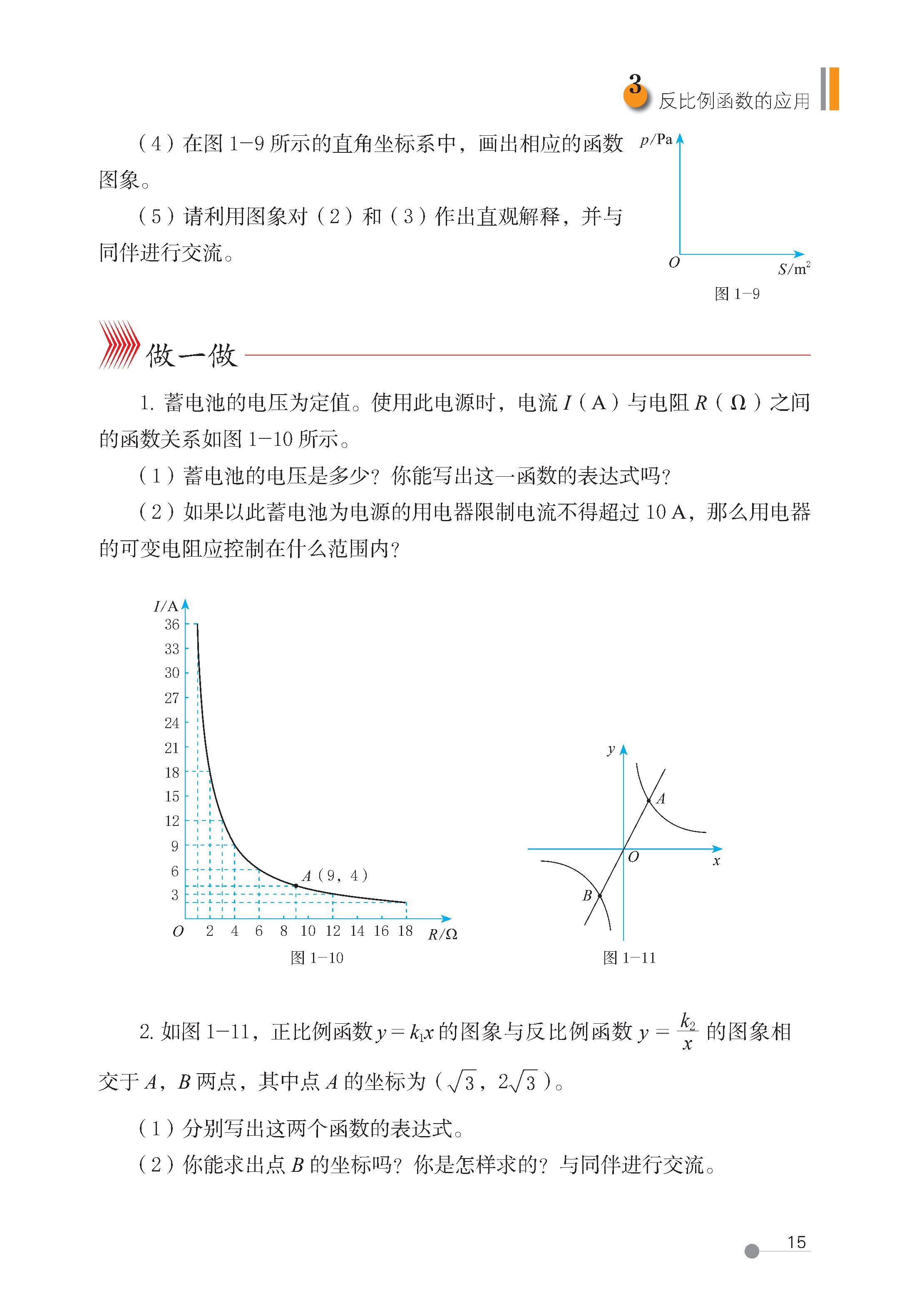
3 反比例函数的应用

第二章 直角三角形的边角关系

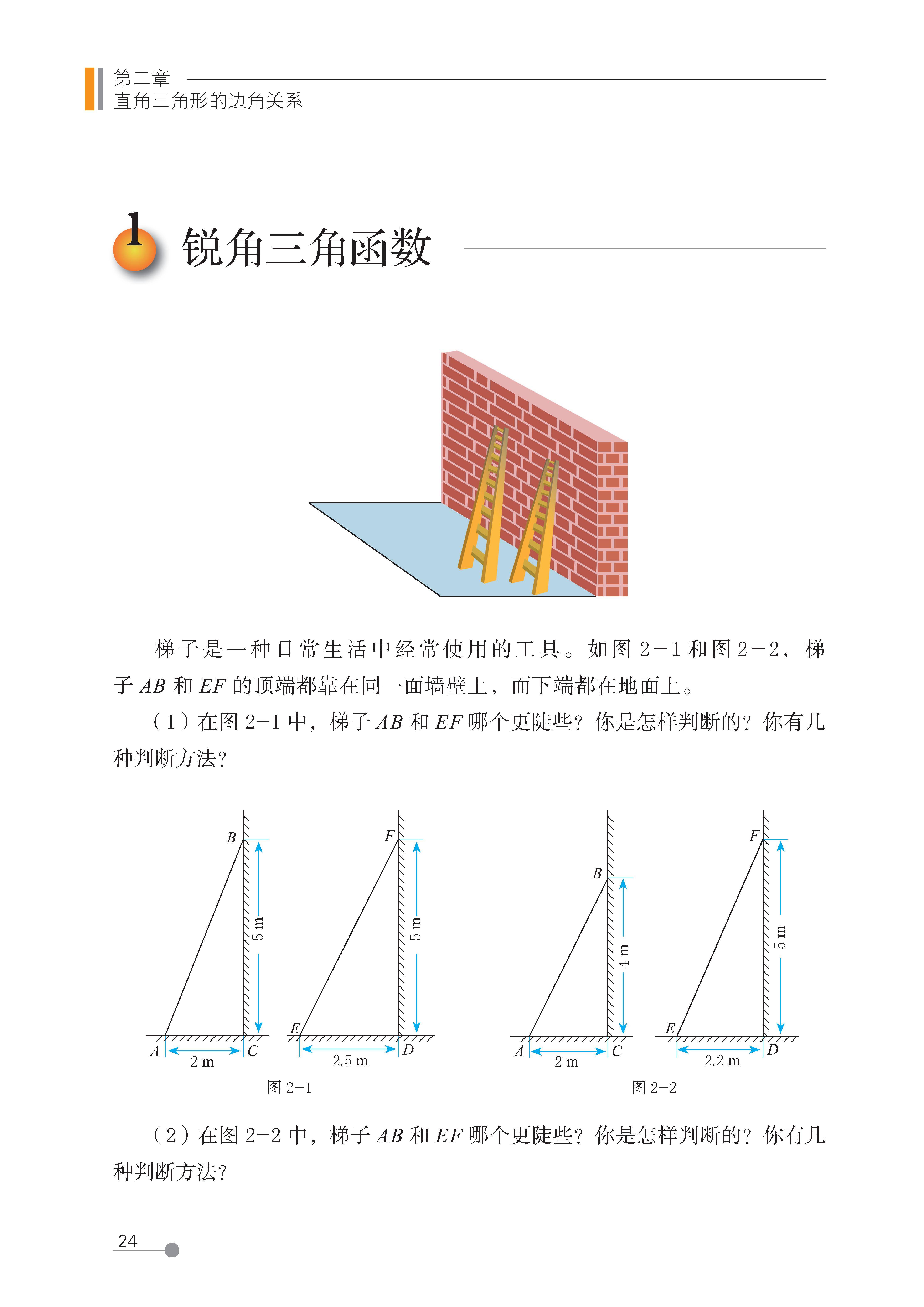
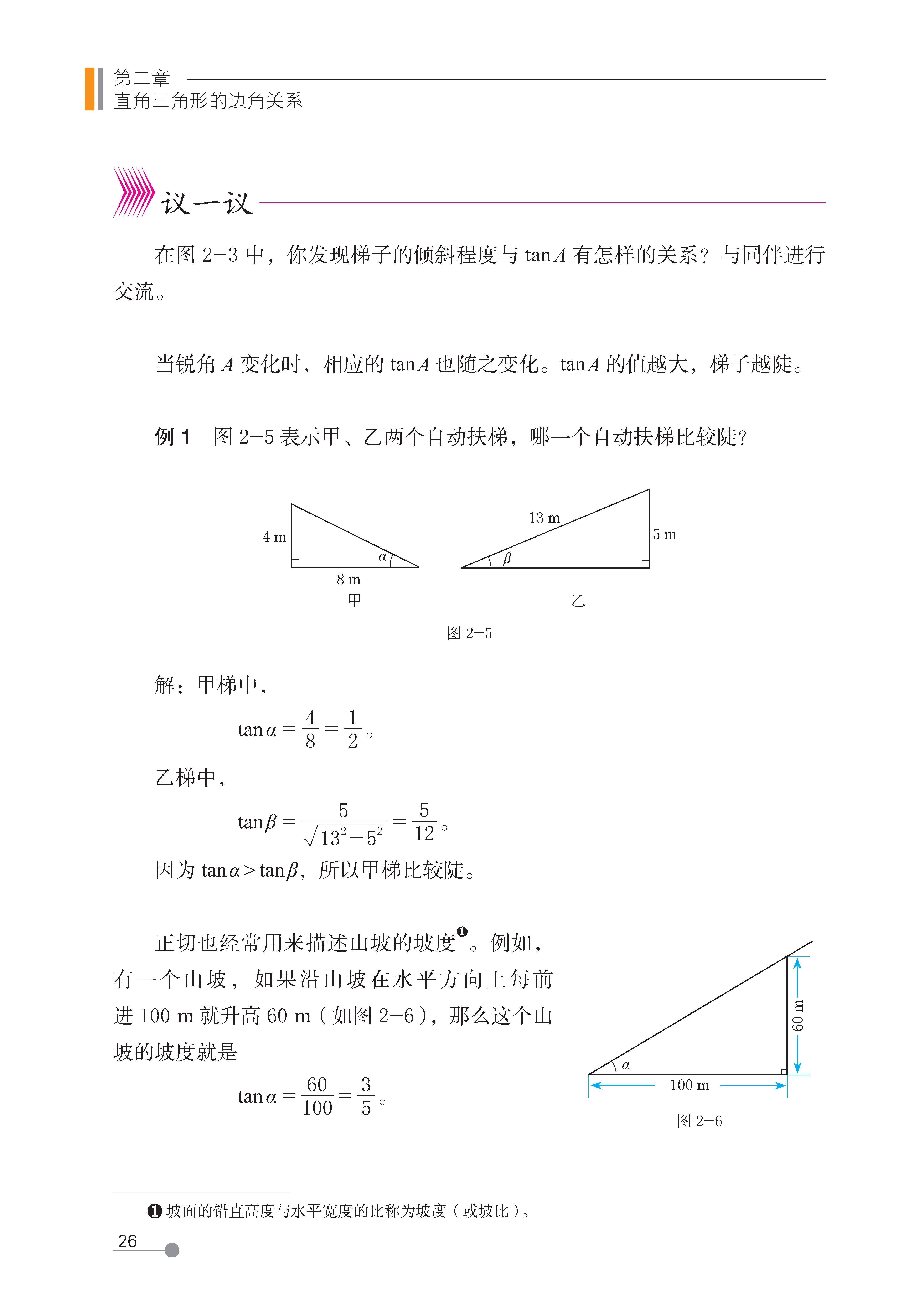
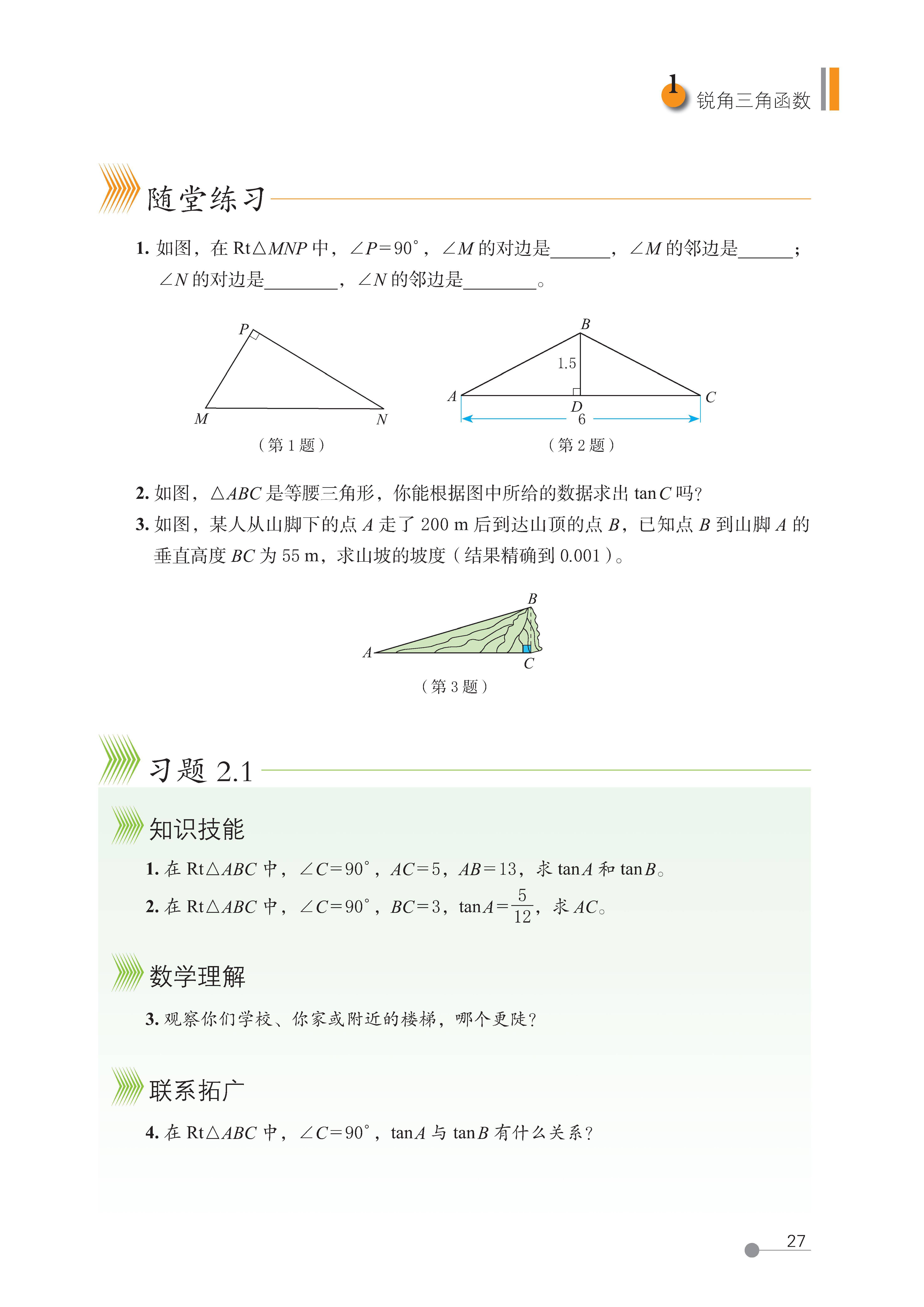
1 锐角三角函数

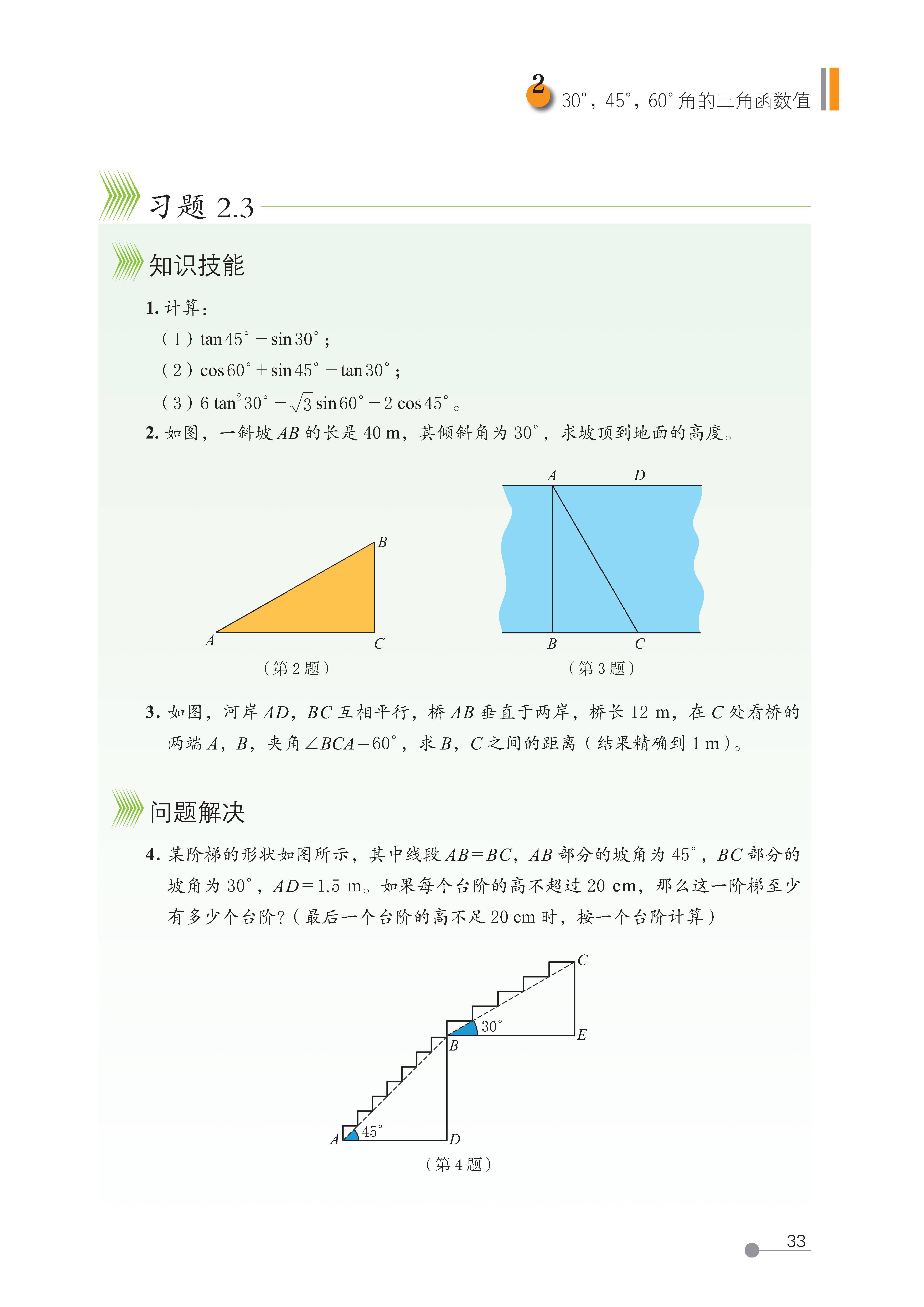
2 30°，45°，60° 的三角函数值

3 用计算器求锐角的三角函数值

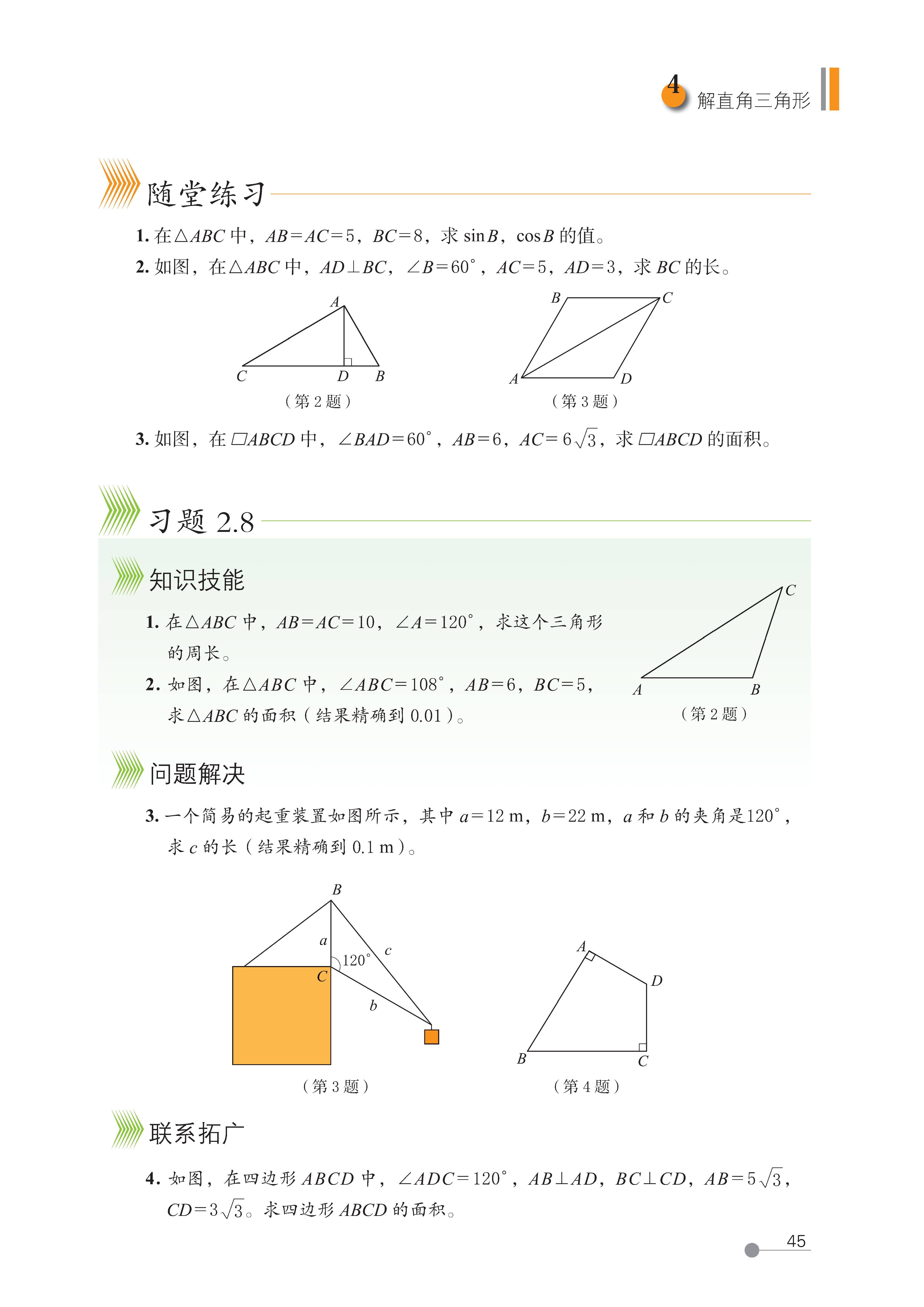
4 解直角三角形

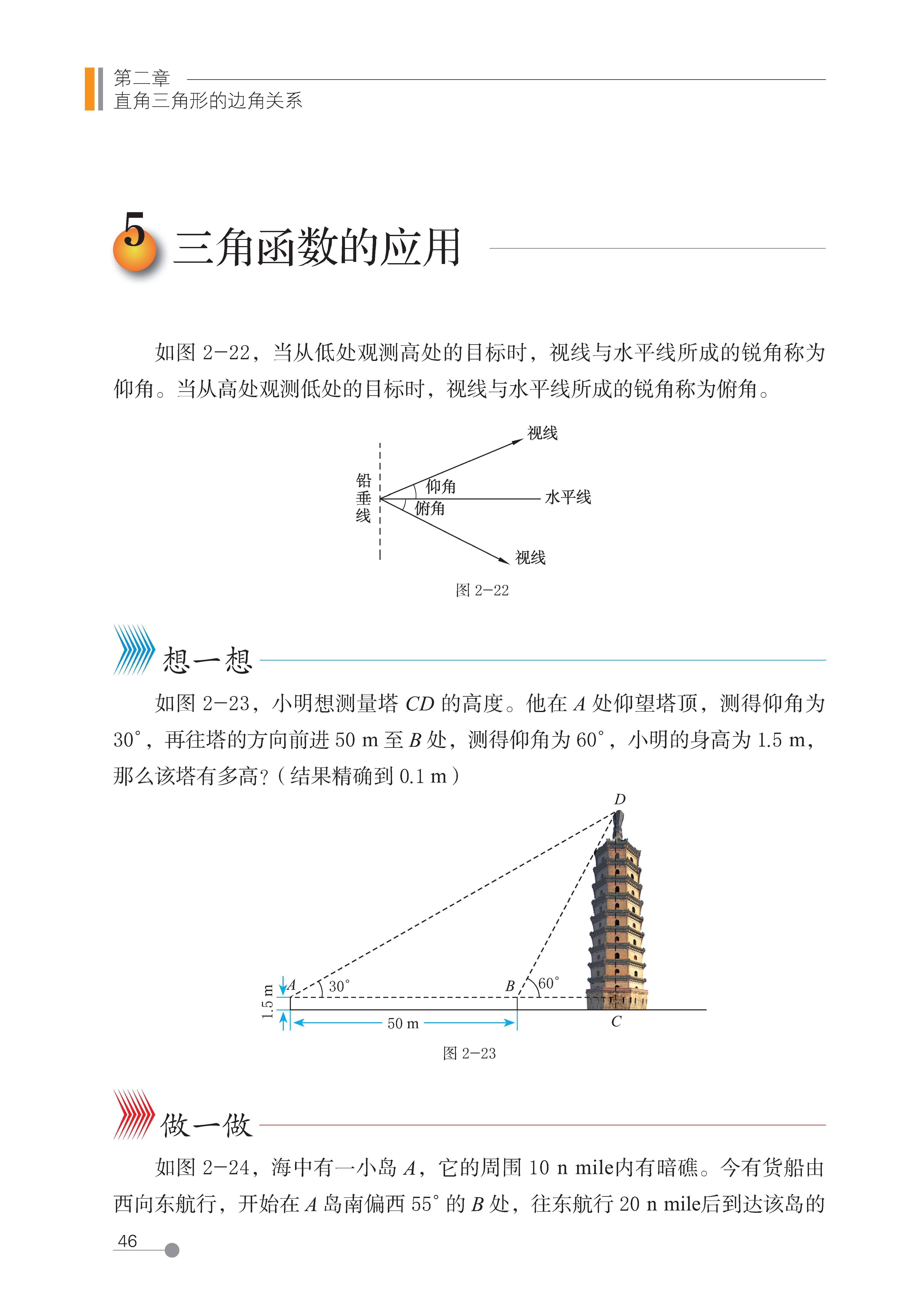
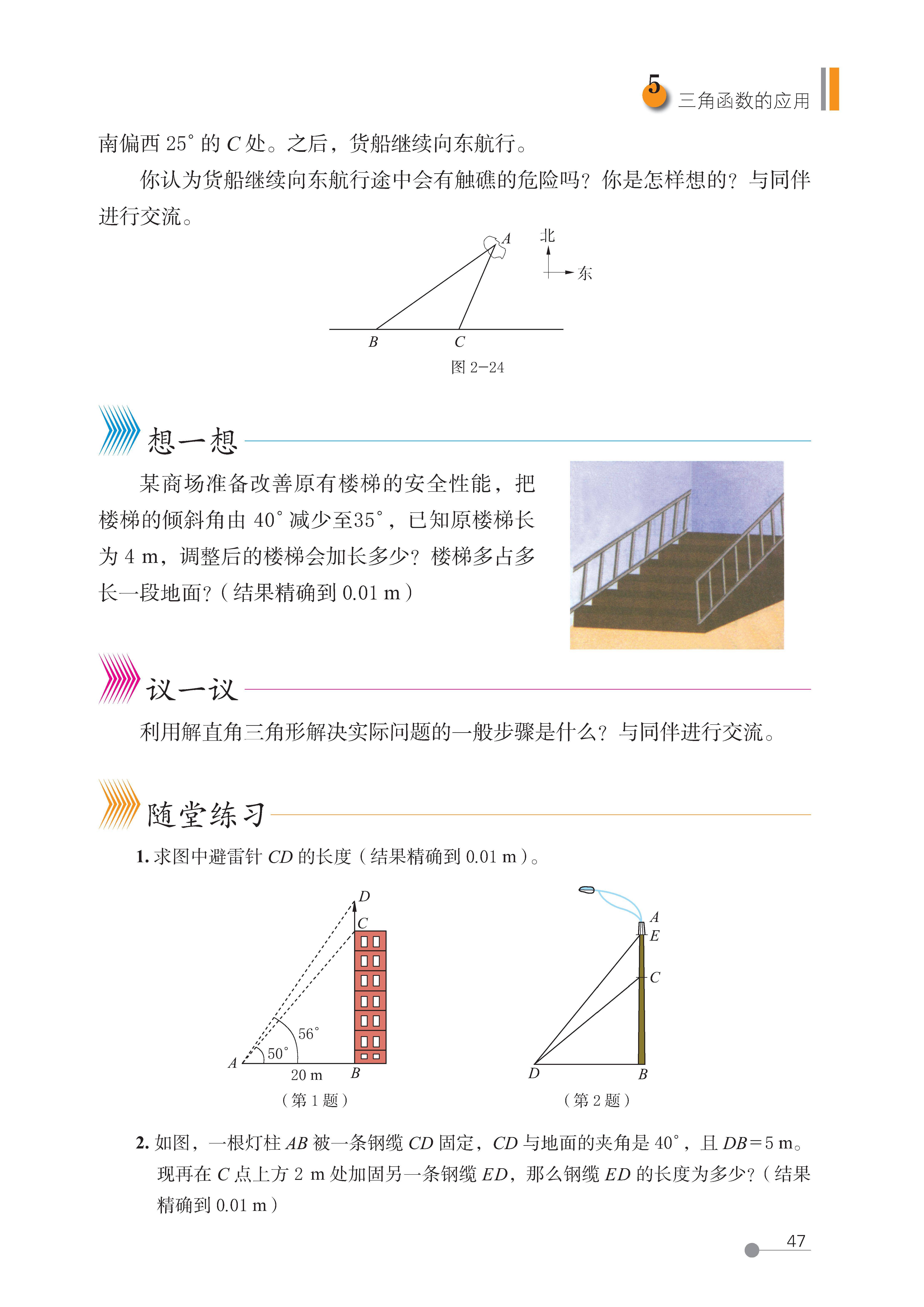
5 三角函数的应用

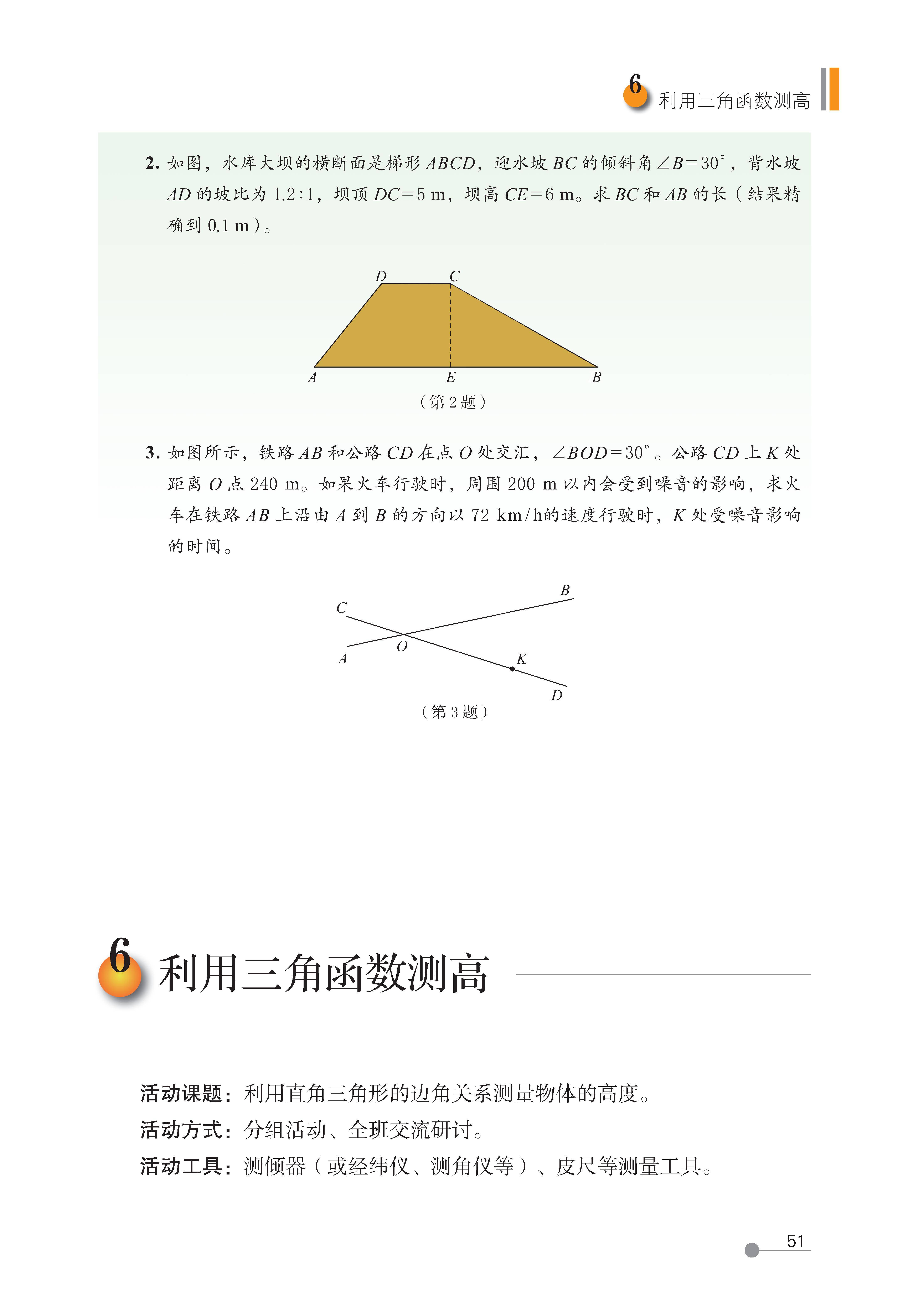
6 利用三角函数测高

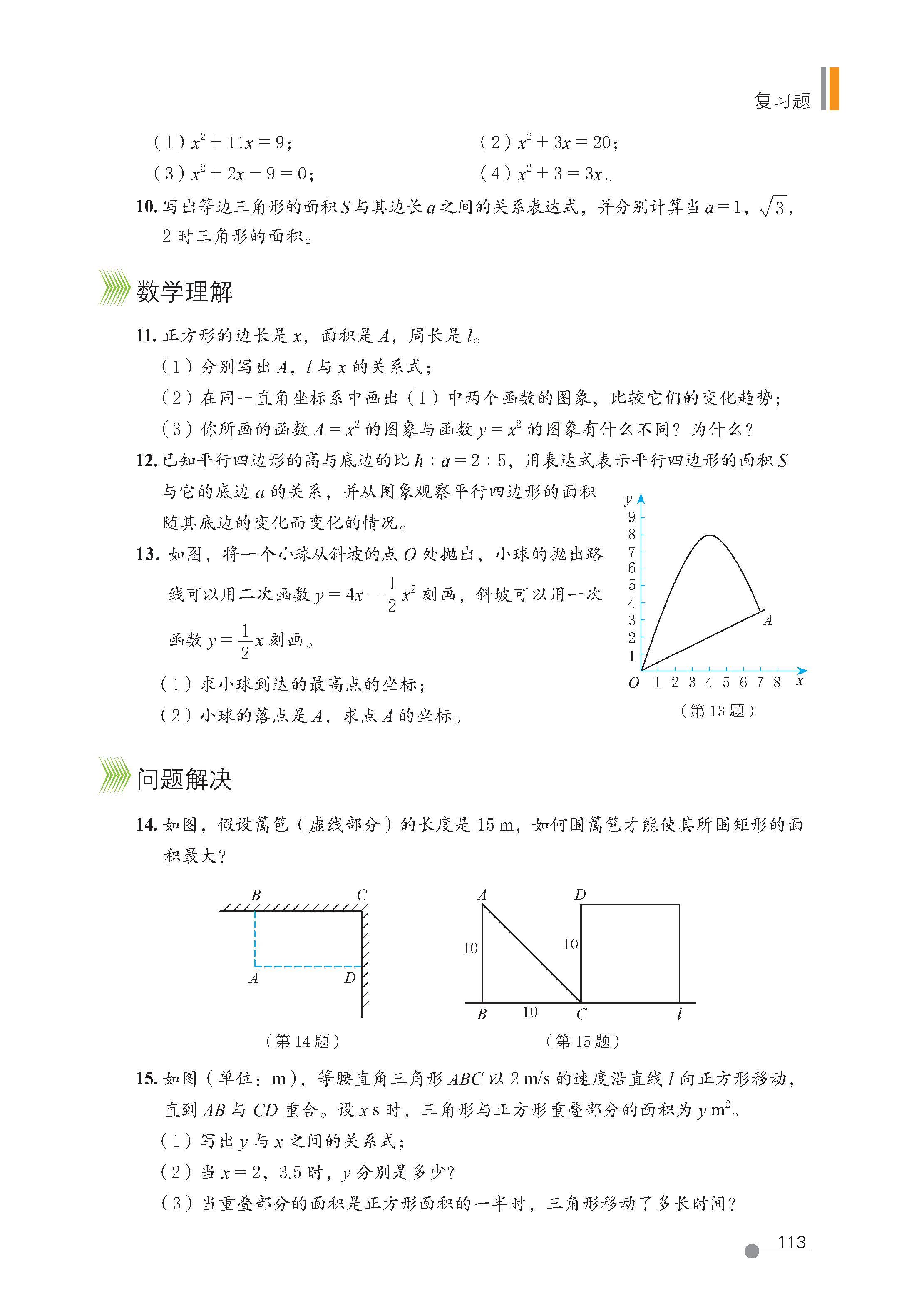
第三章 二次函数

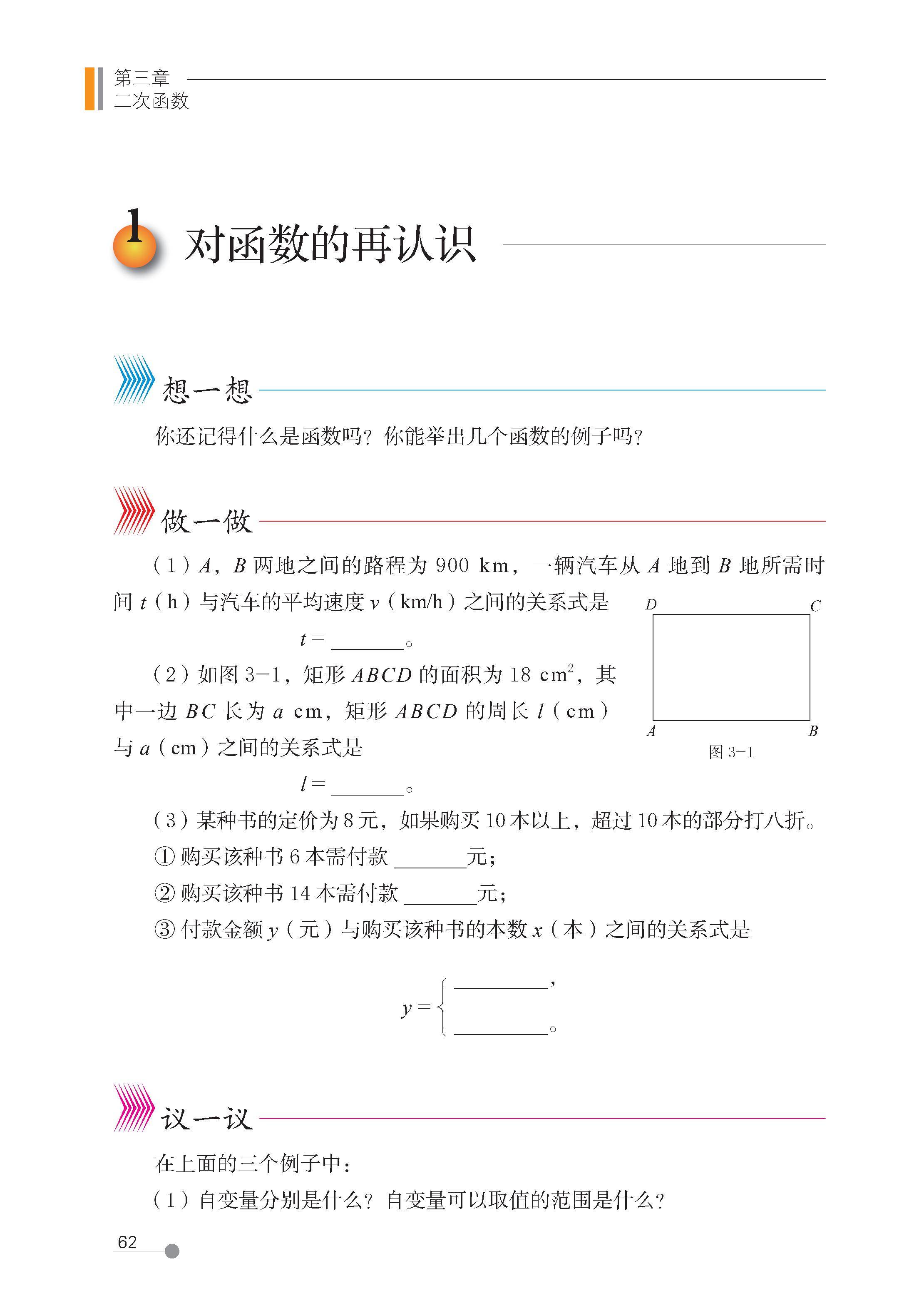
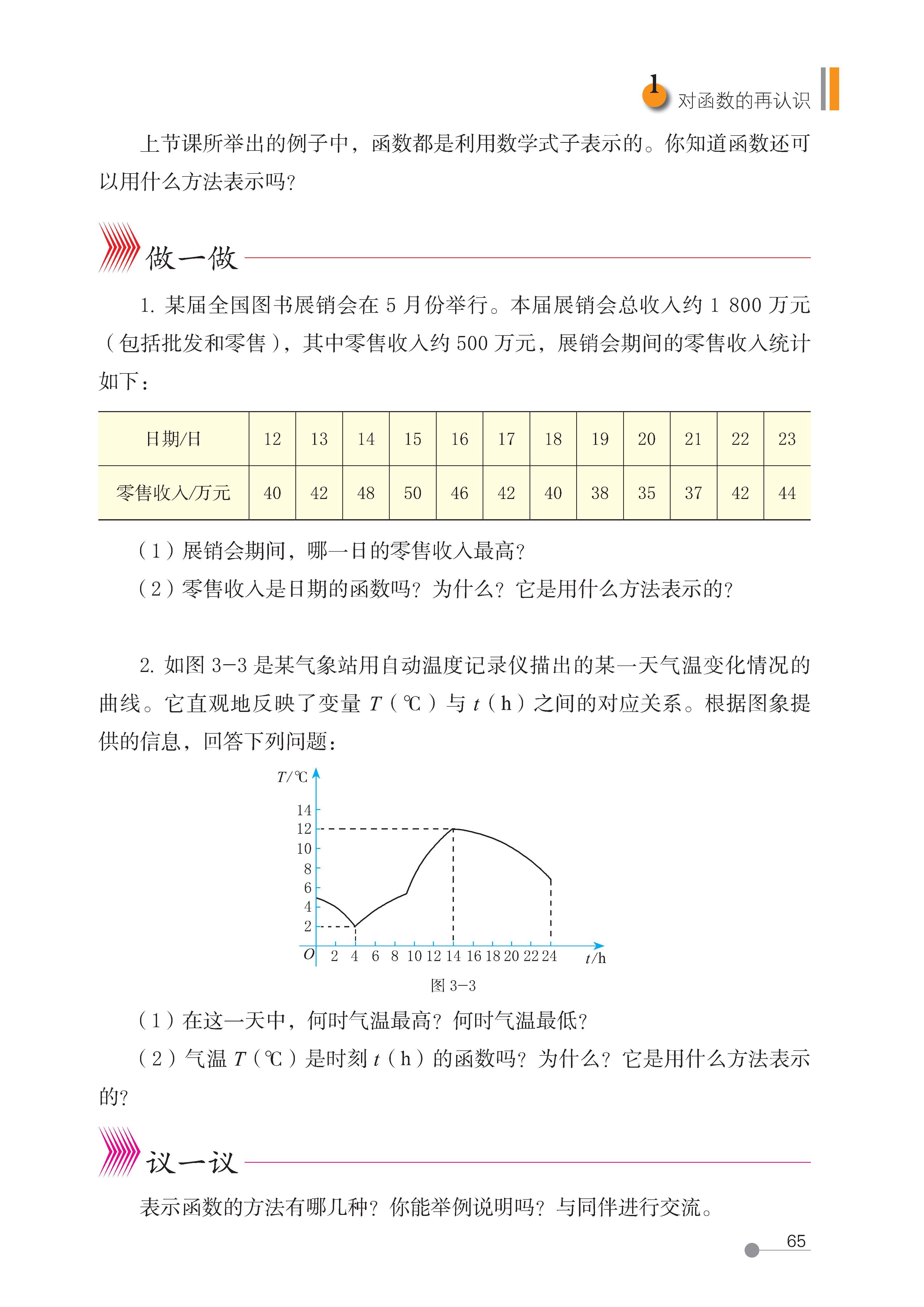
1 对函数的再认识

2 二次函数

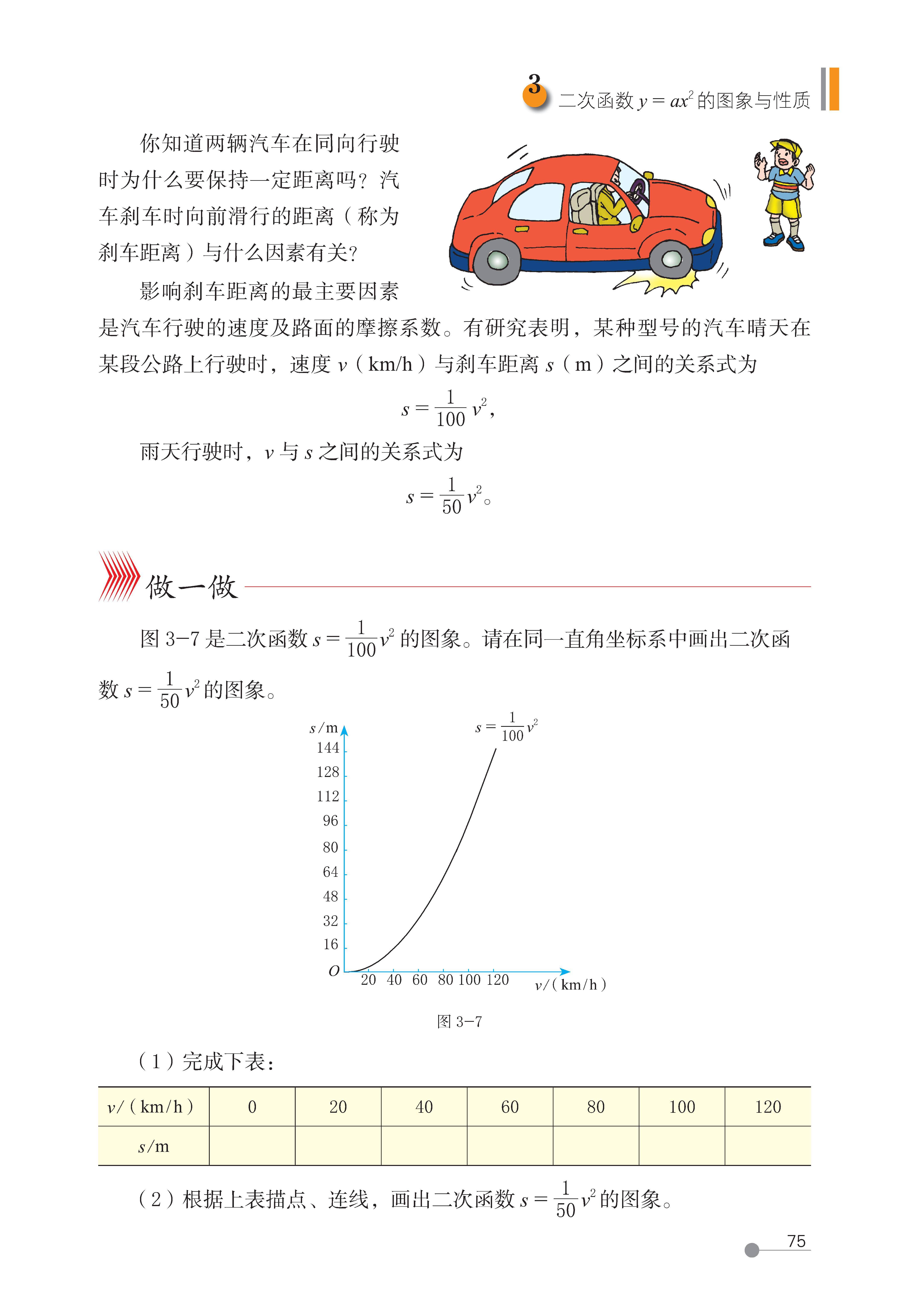
3 二次函数

y=ax

2

的图象和性质

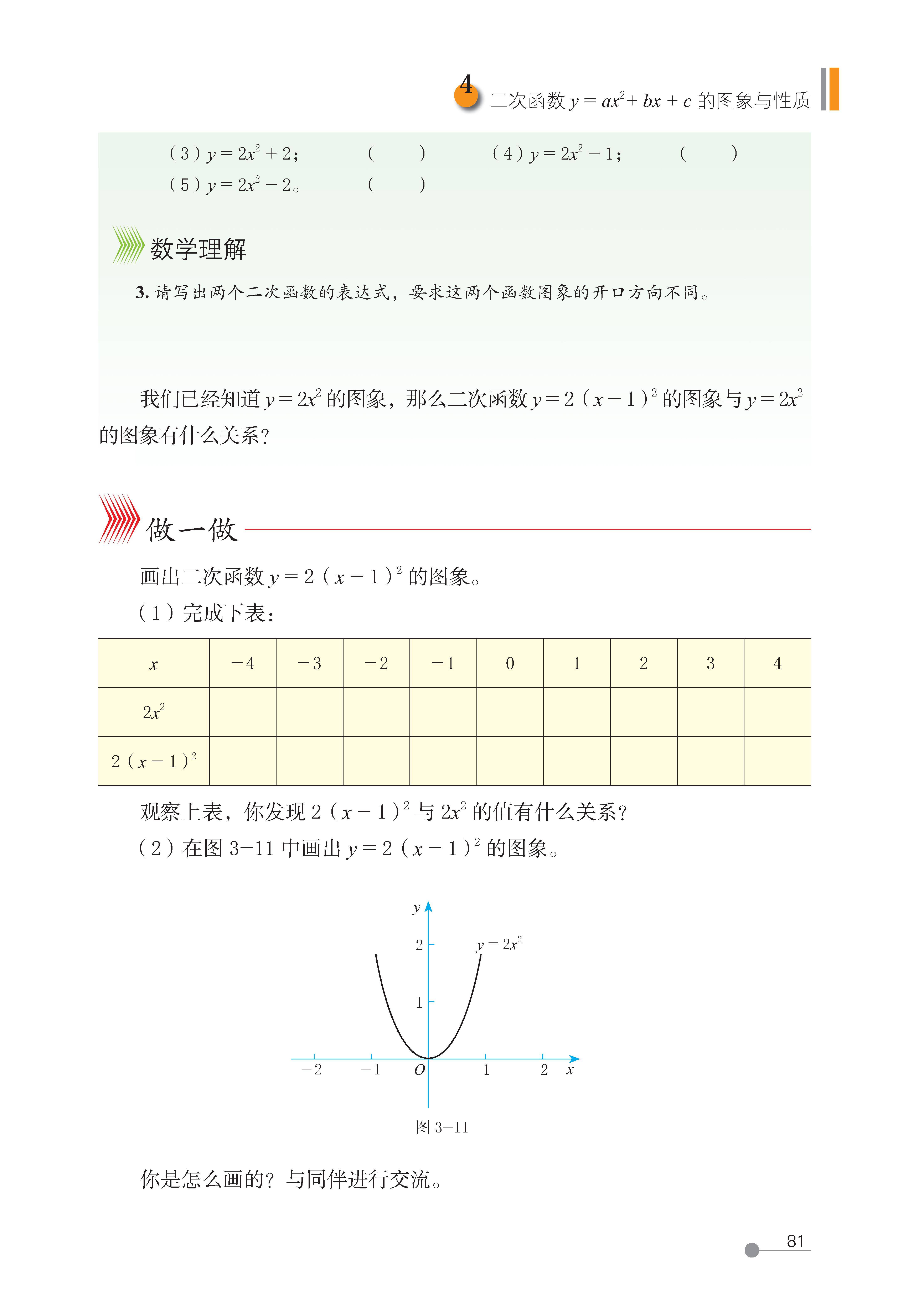
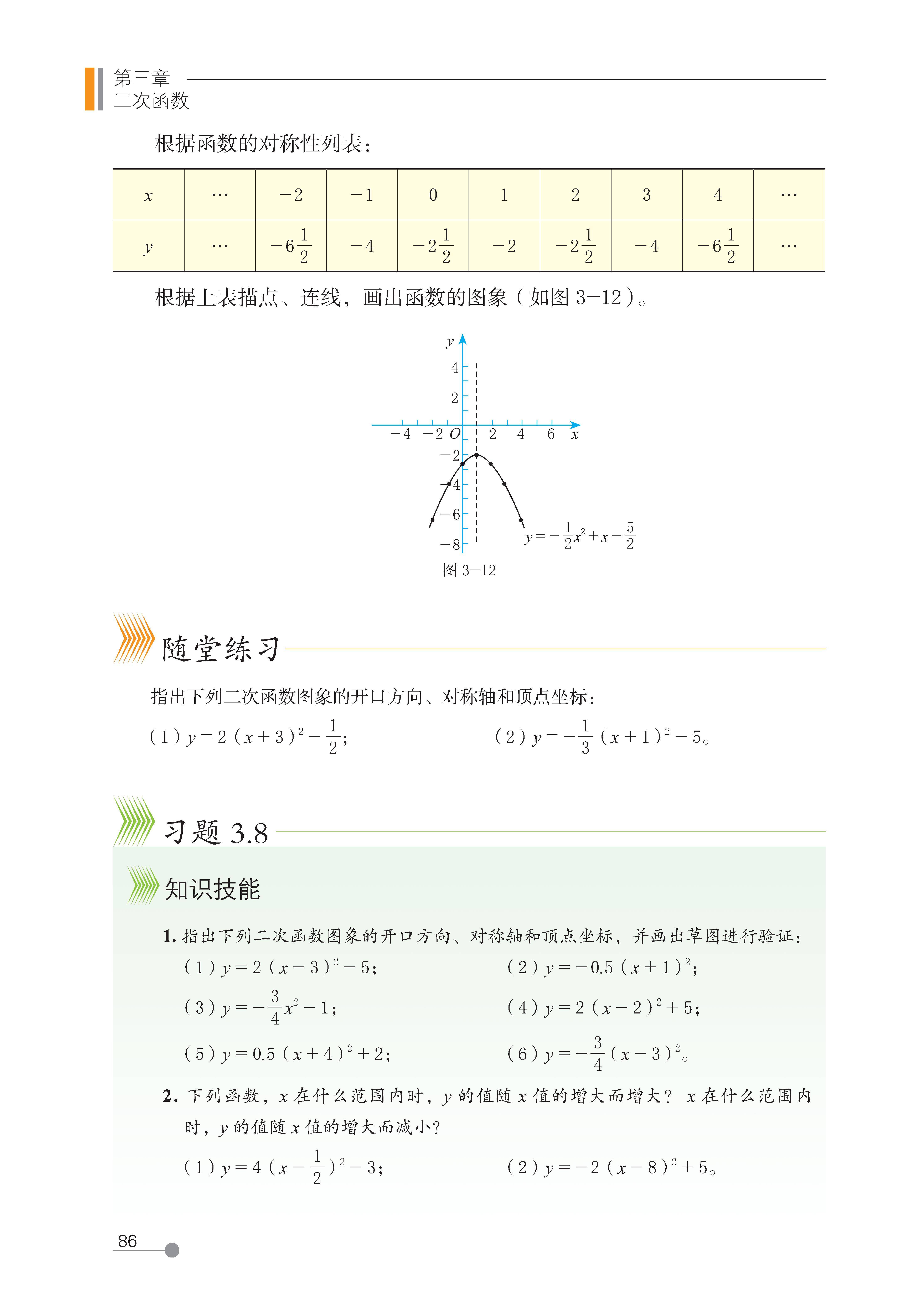
4 二次函数

y=ax

2

+bx+c

的图象和性质

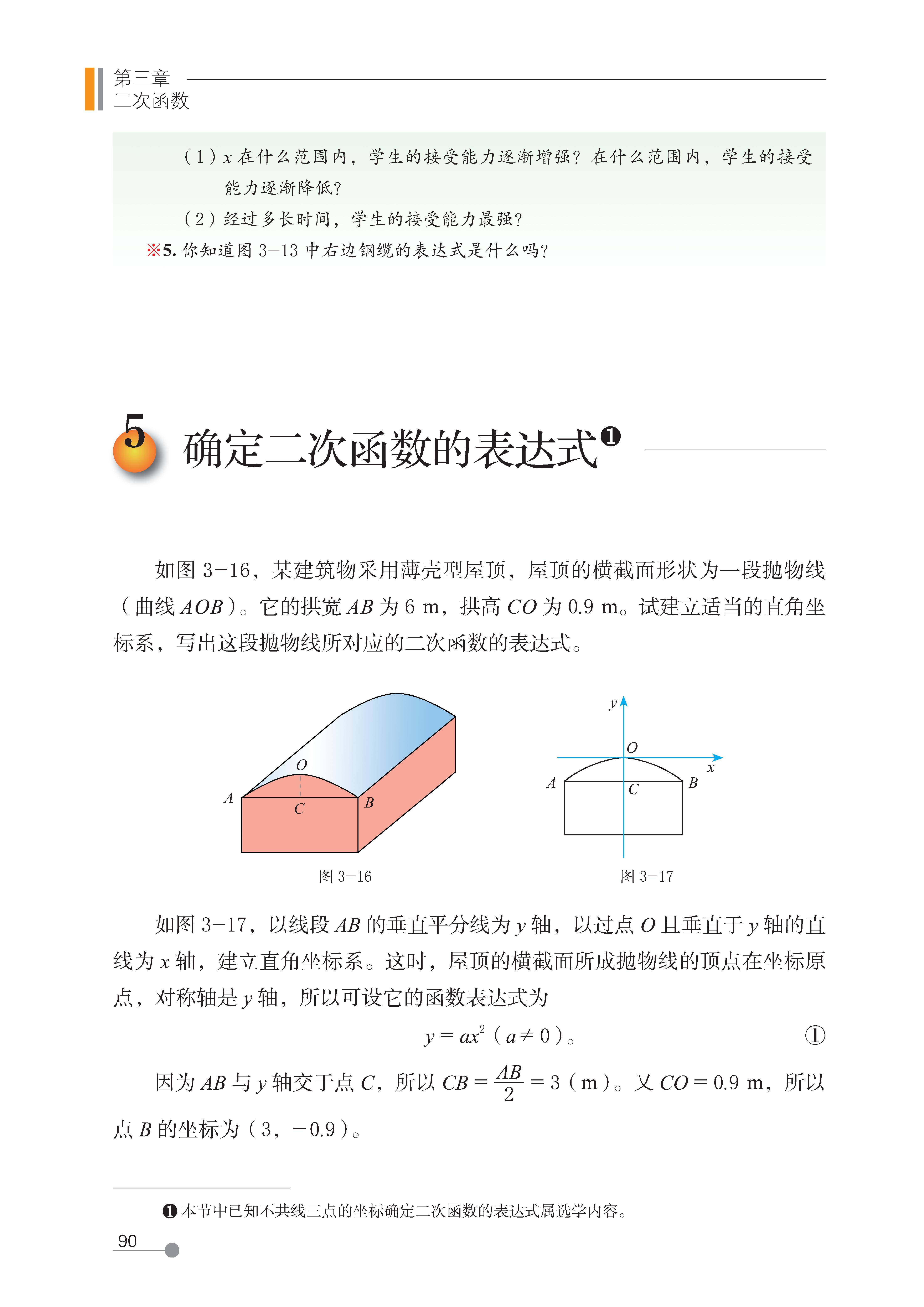
5 确定二次函数的表达式

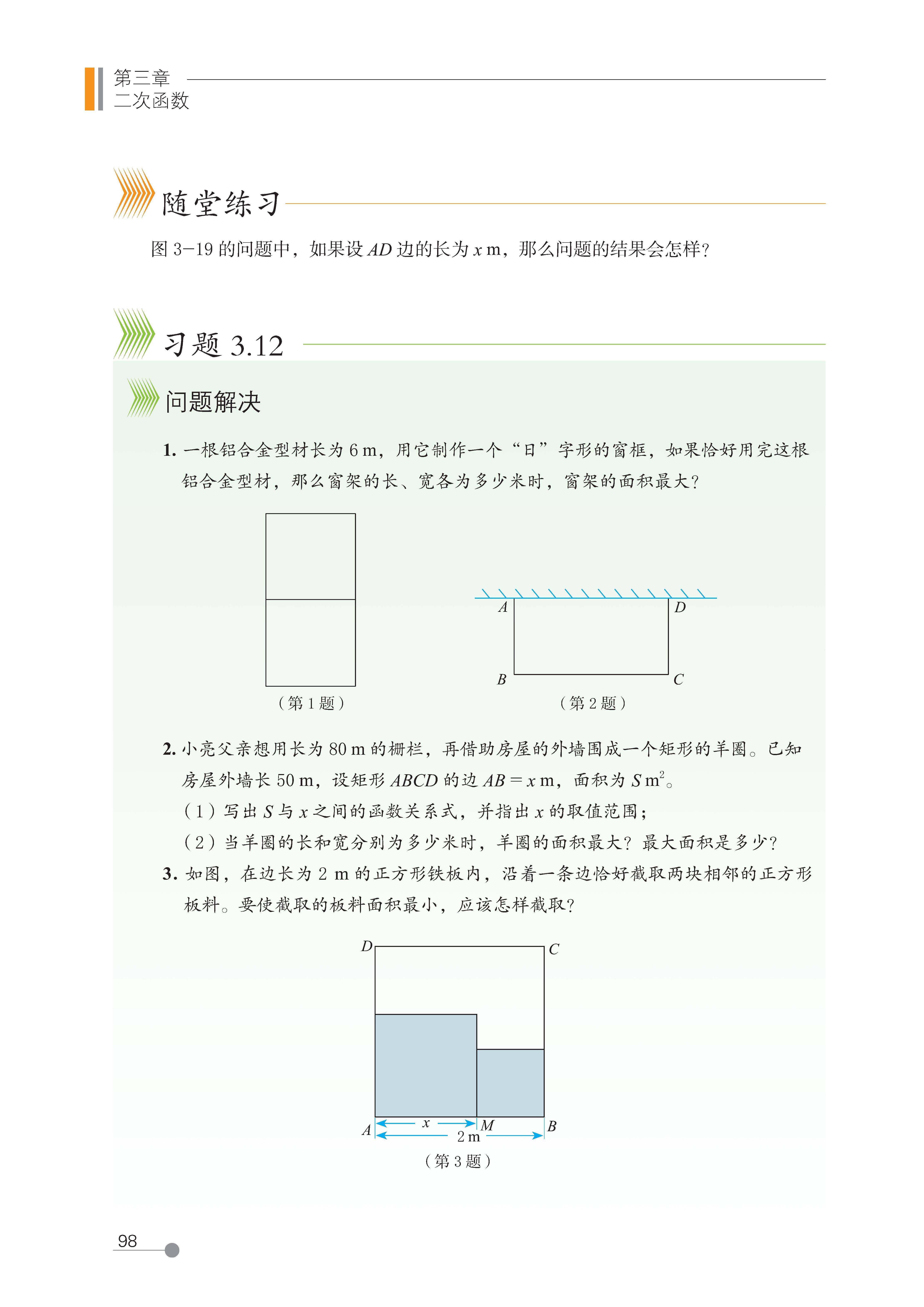
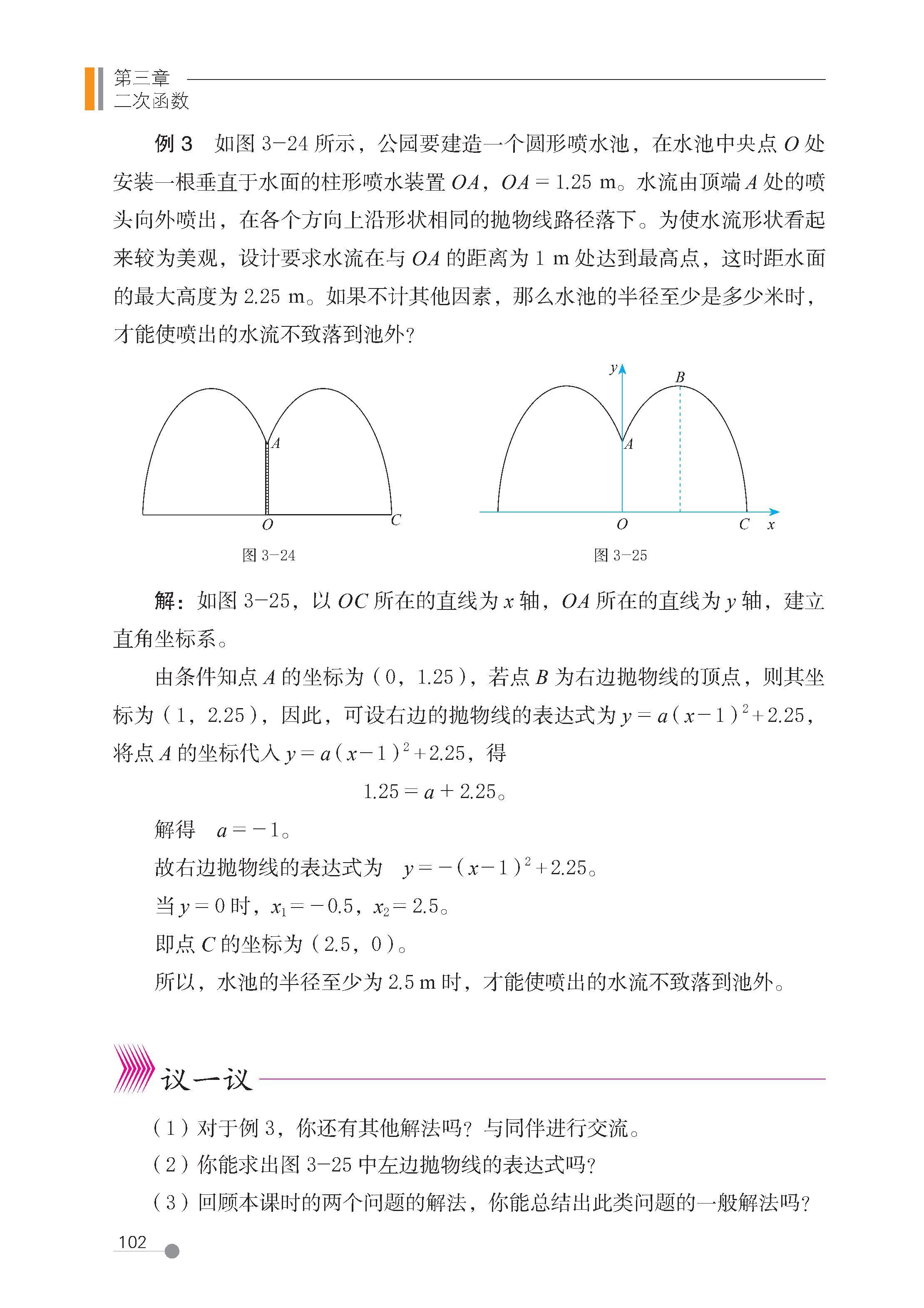
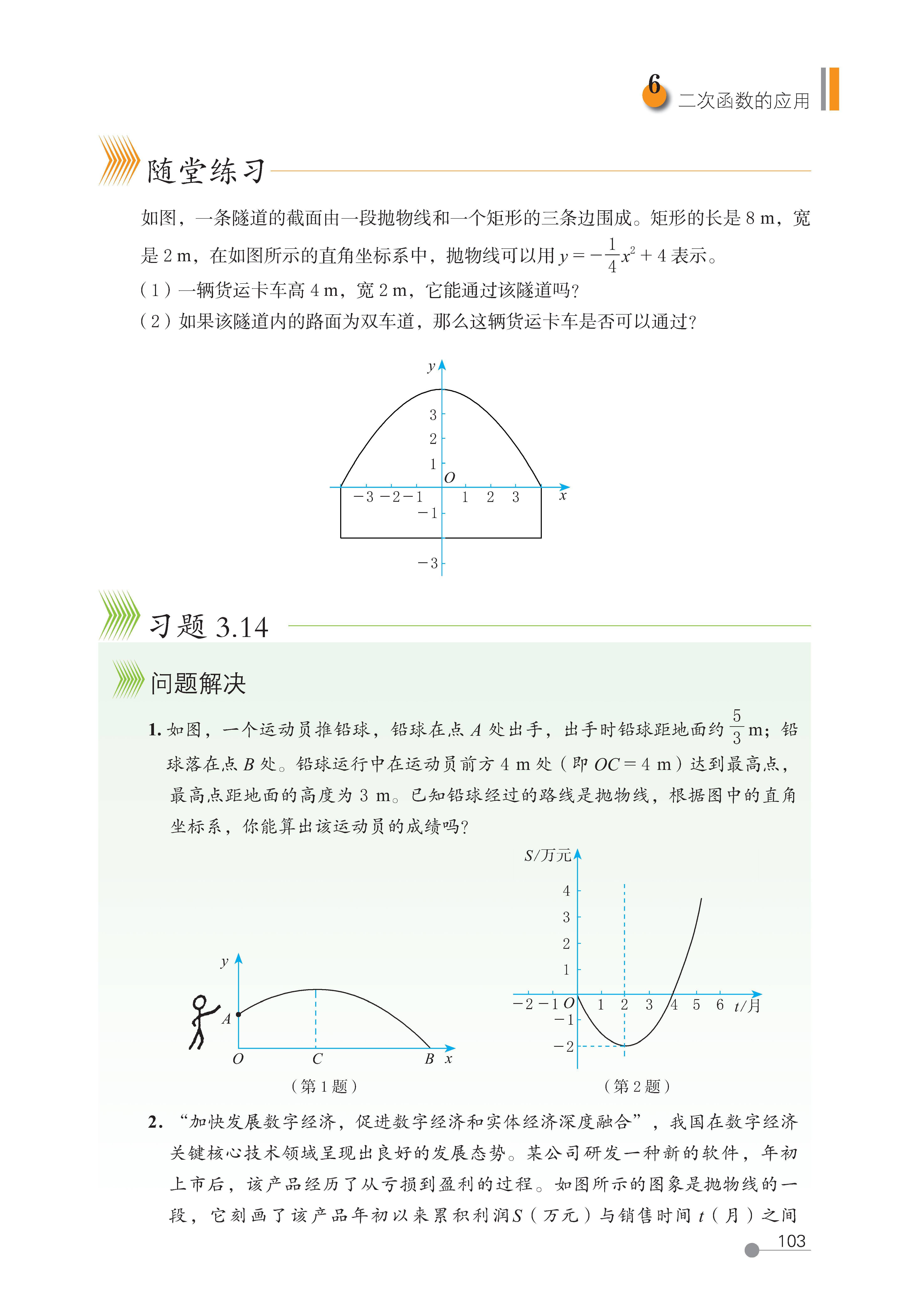
6 二次函数的应用

7 二次函数与一元二次方程

第四章 投影与视图

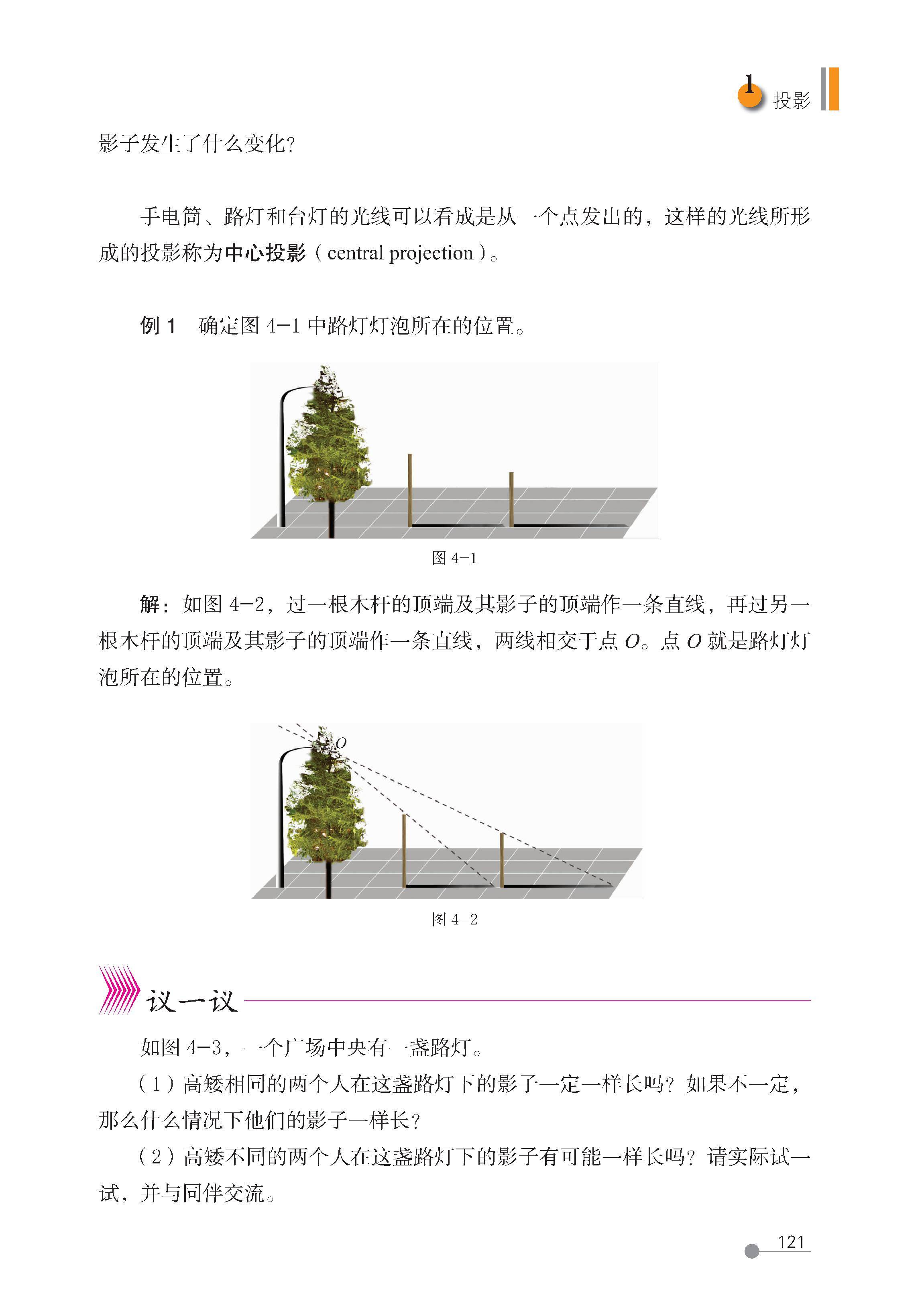
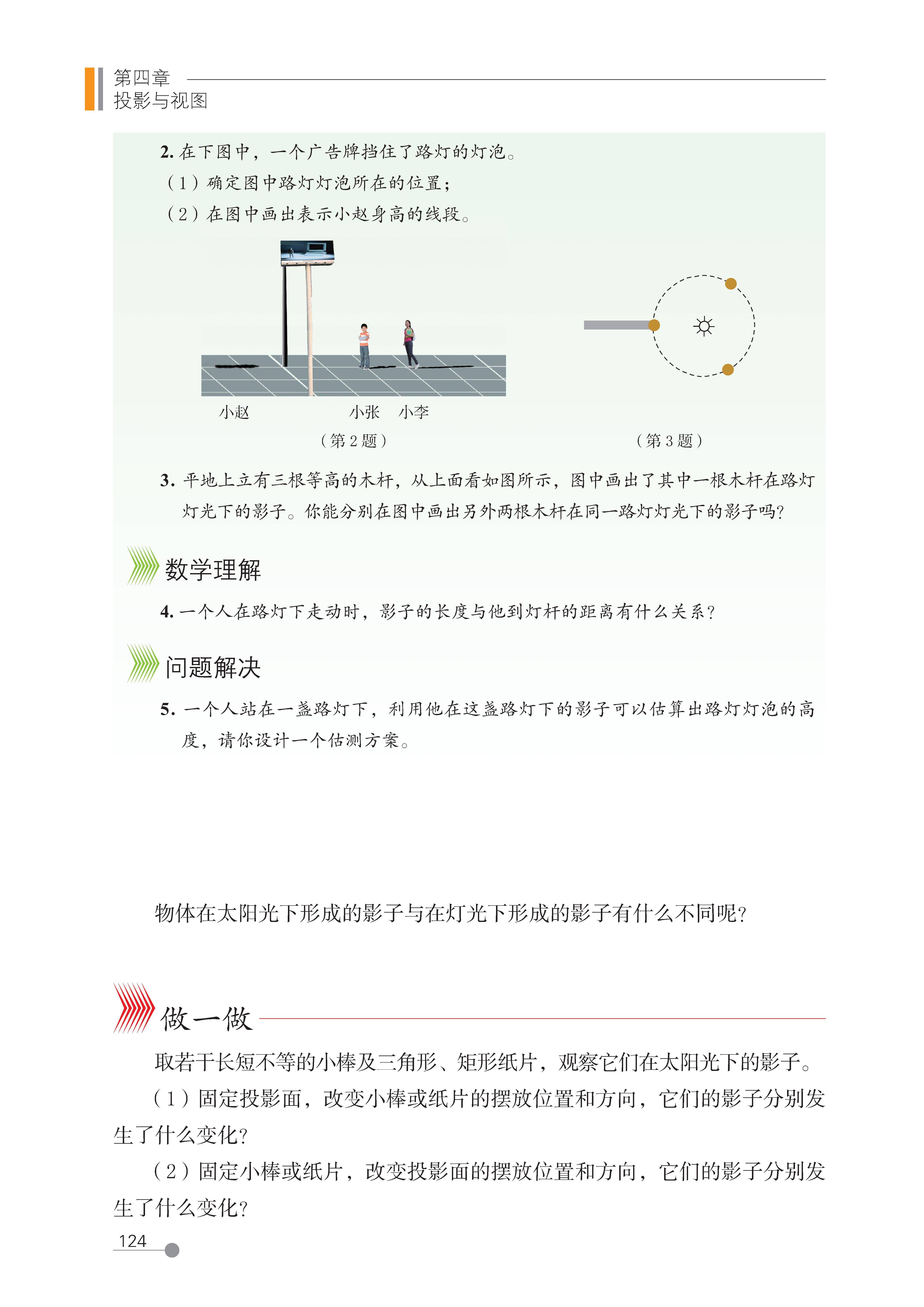
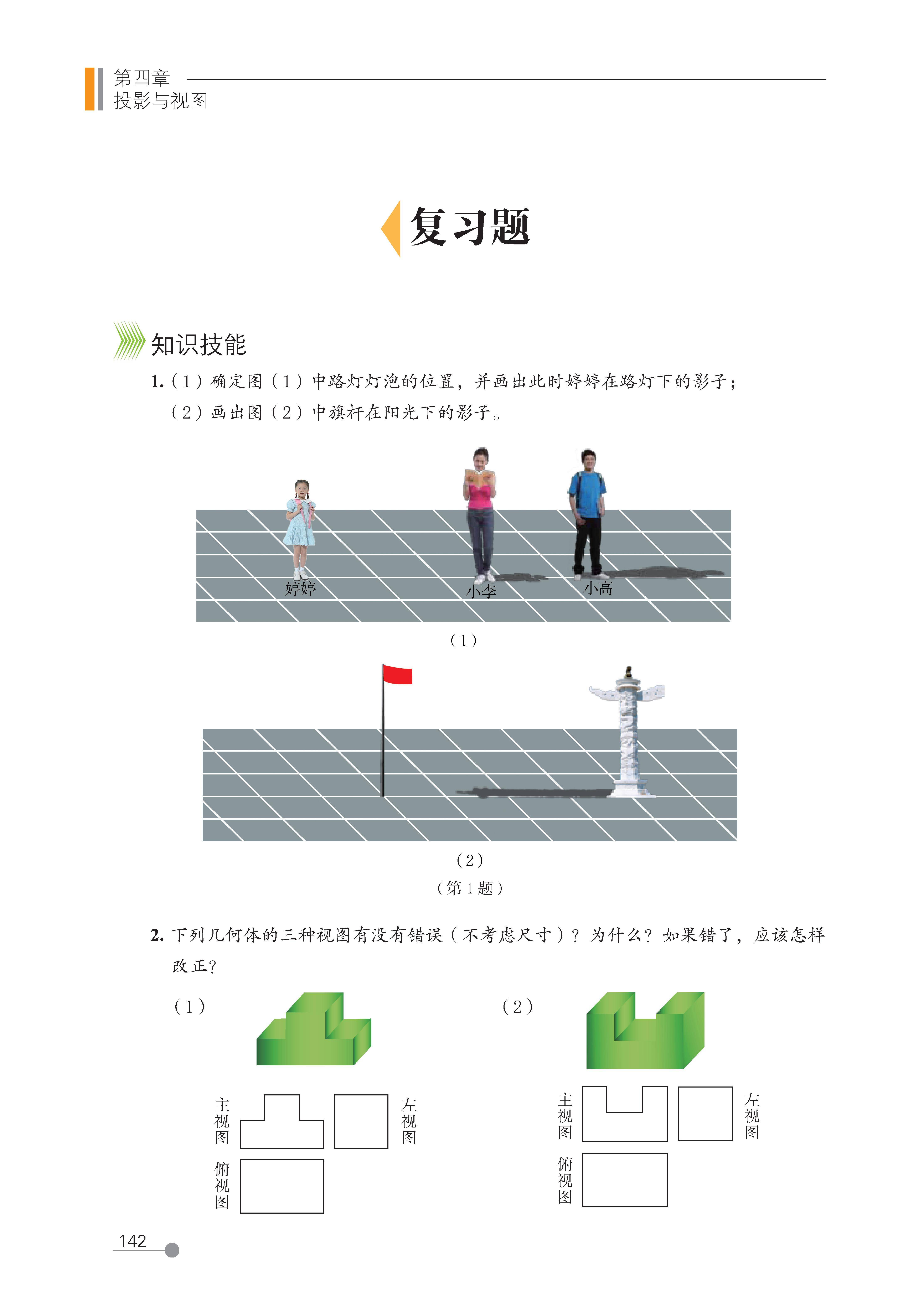
1 投影

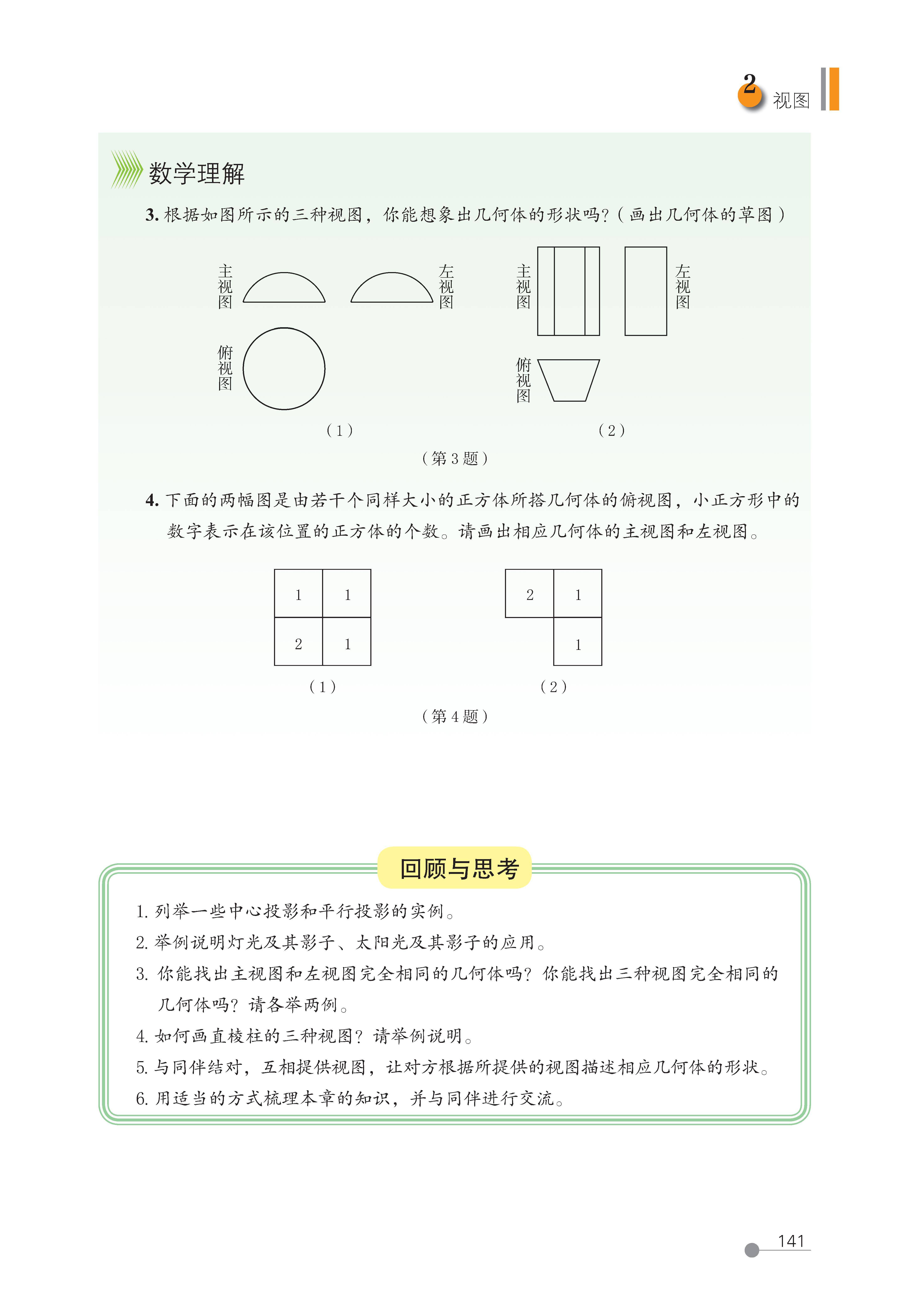
2 视图

鲁教版九年级上册数学第四章 “投影与视图” 是几何知识从 “平面” 向 “立体” 深化的关键章节，核心是培养学生的空间想象能力和从不同视角分析立体图形的能力，其学习重点可围绕 “投影” 和 “视图” 两大模块展开，具体拆解如下：

一、第一部分：投影（第 1 节）—— 理解 “立体图形→平面影子” 的转化逻辑

投影是 “视图” 的基础，核心是掌握 “不同投影方式下，立体图形与投影的关系”，重点包括以下 3 点：

1. 投影的基本概念与分类（明确 “是什么”）

核心定义：用光线照射物体，在某个平面（如地面、墙壁）上得到的影子叫做物体的投影；照射光线叫做投影线；投影所在的平面叫做投影面。

分类与关键特征（高频考点，需对比区分）：

投影类型 投影线特点 核心性质 常见应用场景

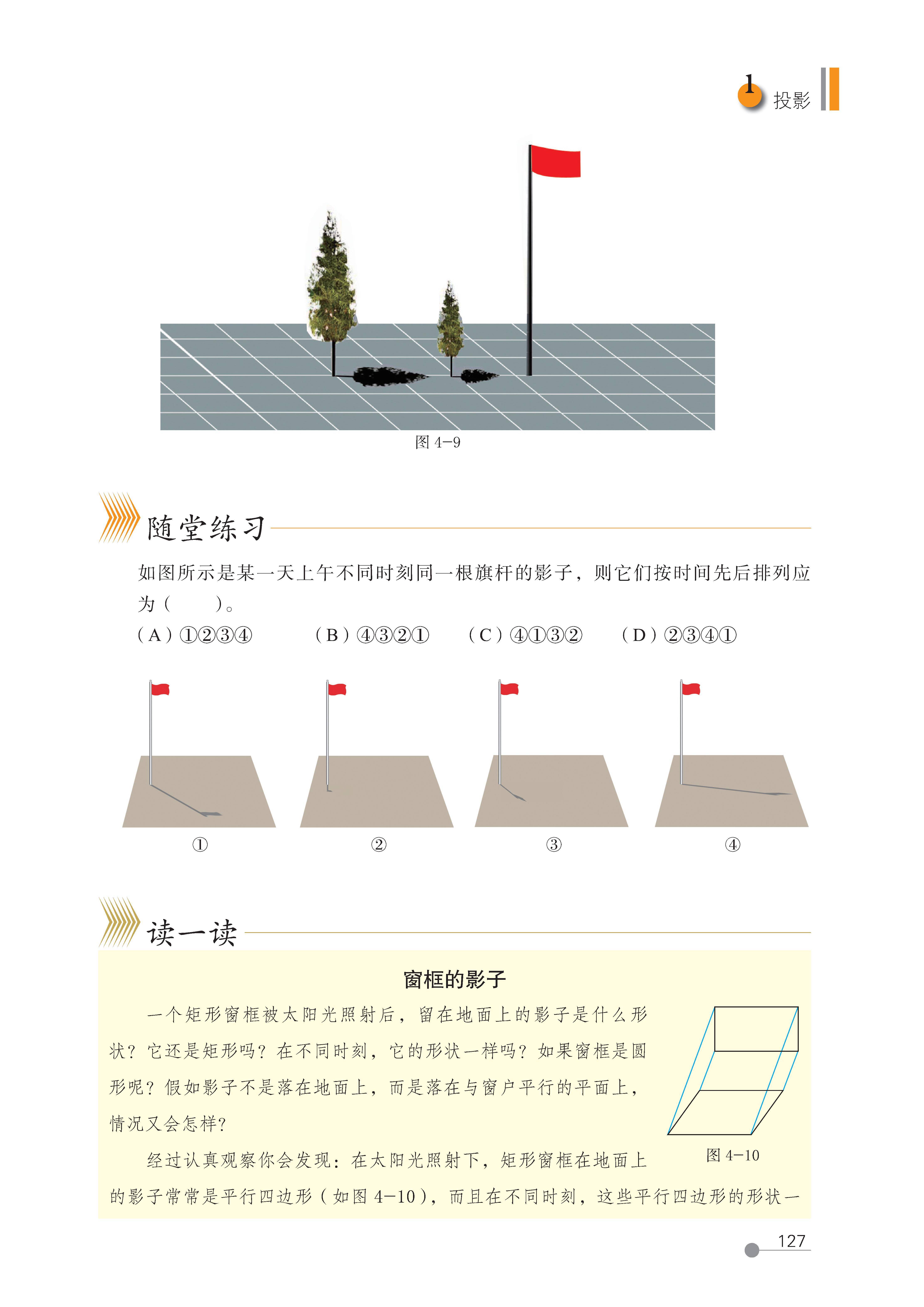
平行投影 投影线互相平行 ① 同一时刻，平行光线照射下，不同物体的影子方向相同；

② 物体高度与影长的比是定值（可用于测量物体高度） 太阳光照射（太阳光可近似看作平行光线）

中心投影 投影线相交于一点（投影中心） ① 同一投影中心下，物体离投影中心越近，影子越小；离投影中心越远，影子越大；

② 不同物体的影子方向可能不同 灯光、手电筒照射（光源为点，投影线从点出发）

易错区分：判断投影类型的关键 —— 看 “投影线是否平行”，而非 “影子的形状”。

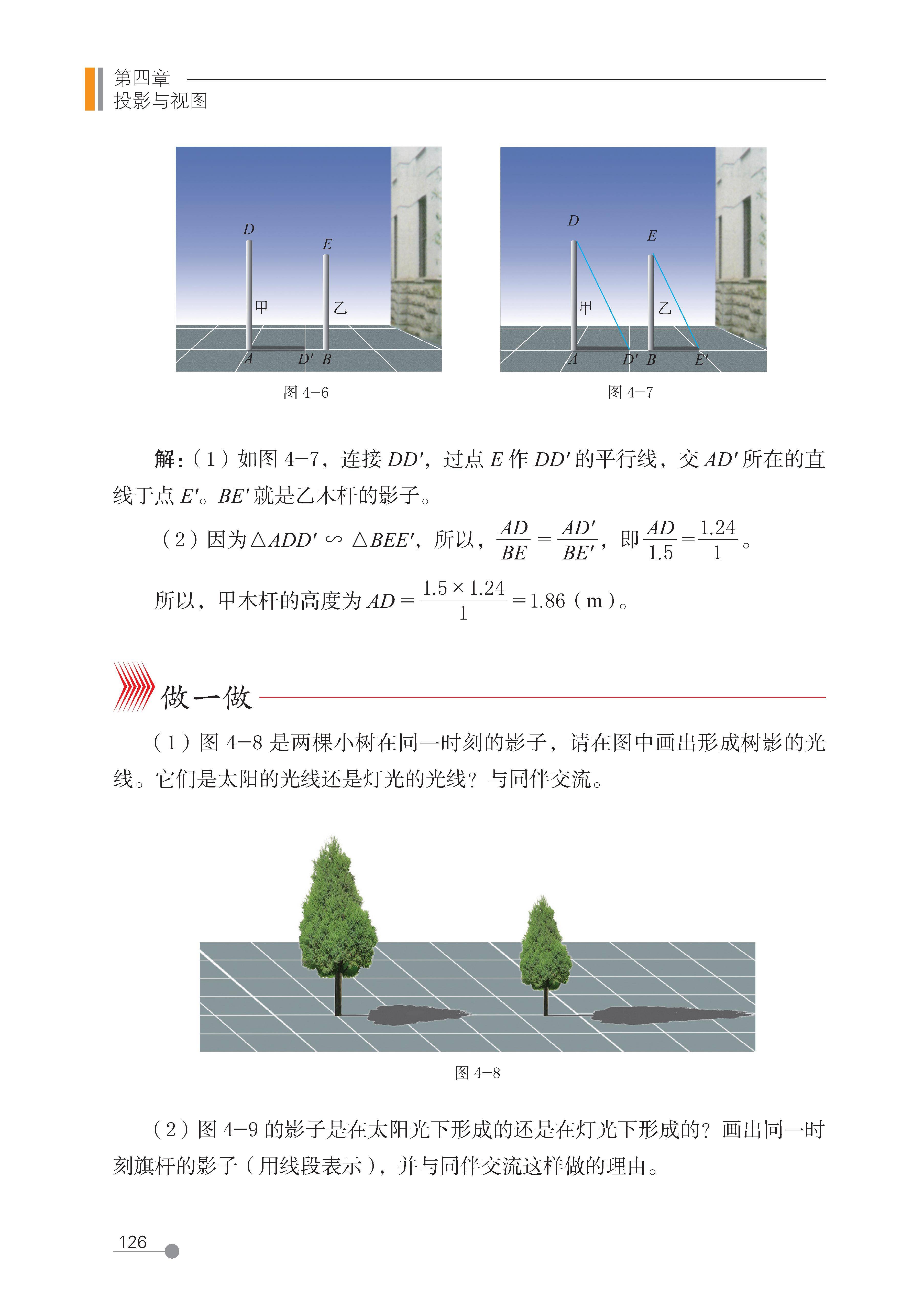
2. 平行投影的应用（重点是 “太阳光下的影长计算”）

核心原理：同一时刻，太阳光下所有垂直于地面的物体，其 “物体高度 / 影长” 的值相等（因为投影线平行，构成相似三角形）。

典型题型：利用影长测量物体高度（如测旗杆高度），步骤为：

测量已知高度物体的影长（如身高 1.6m 的人，影长 1.2m）；

测量目标物体的影长（如旗杆影长 6m）；

设旗杆高度为

h

，根据比例关系列方程：

1.2

1.6

=

6

h

，求解得

h

。

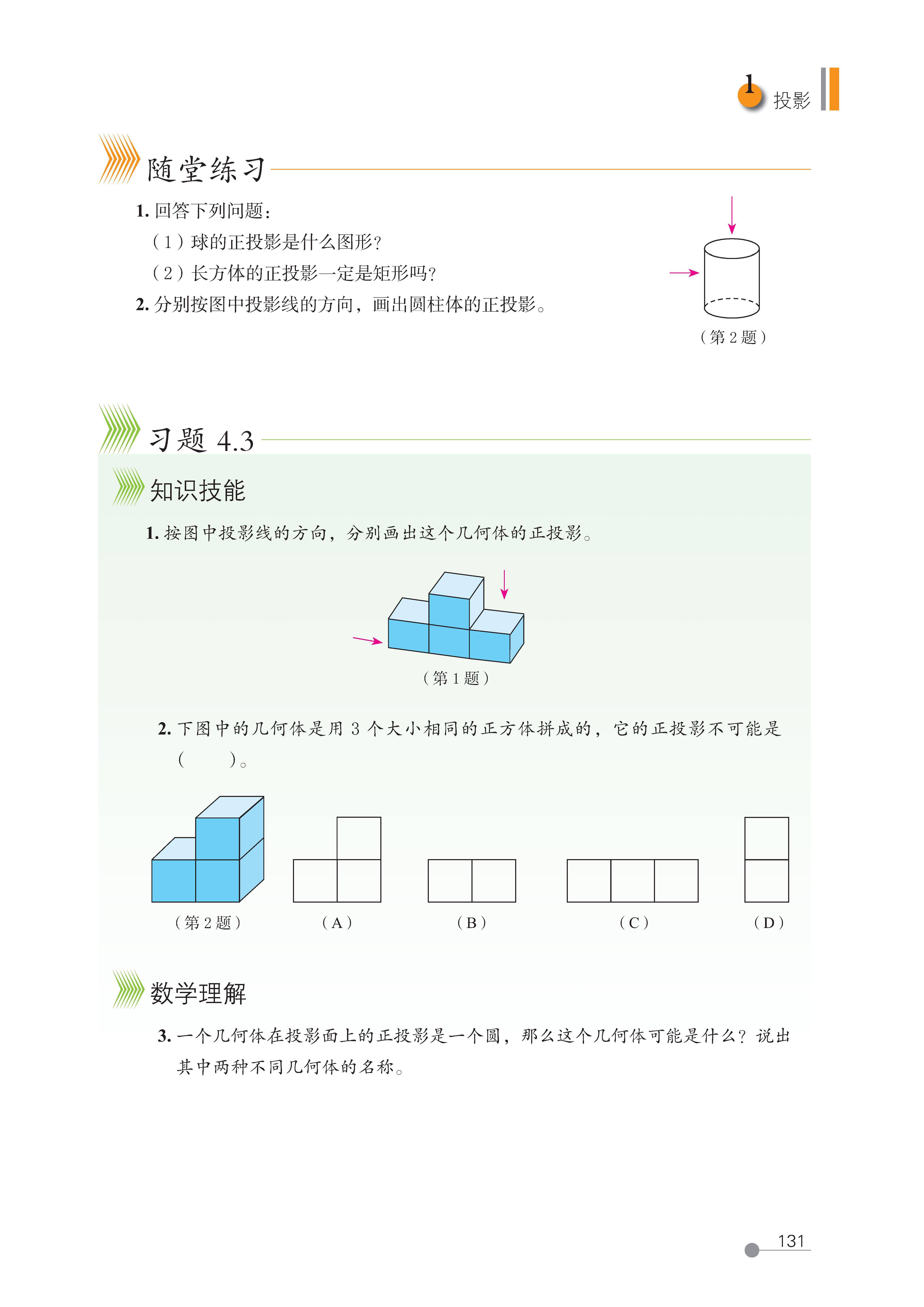
3. 正投影的概念（视图的理论基础）

定义：当平行投影的投影线垂直于投影面时，这种投影叫做正投影（若投影线不垂直于投影面，则为 “斜投影”）。

关键作用：视图（主视图、俯视图、左视图）本质就是 “立体图形在三个互相垂直的投影面上的正投影”，是后续学习视图的核心前提。

二、第二部分：视图（第 2 节）—— 掌握 “立体图形→三个平面视图” 的转化与应用

视图是本章的核心，也是中考高频考点，重点围绕 “三视图的绘制”“由三视图还原立体图形”“视图与几何体的尺寸关联” 展开，具体包括 4 点：

1. 三视图的定义与摆放规则（明确 “三个视图是什么、怎么放”）

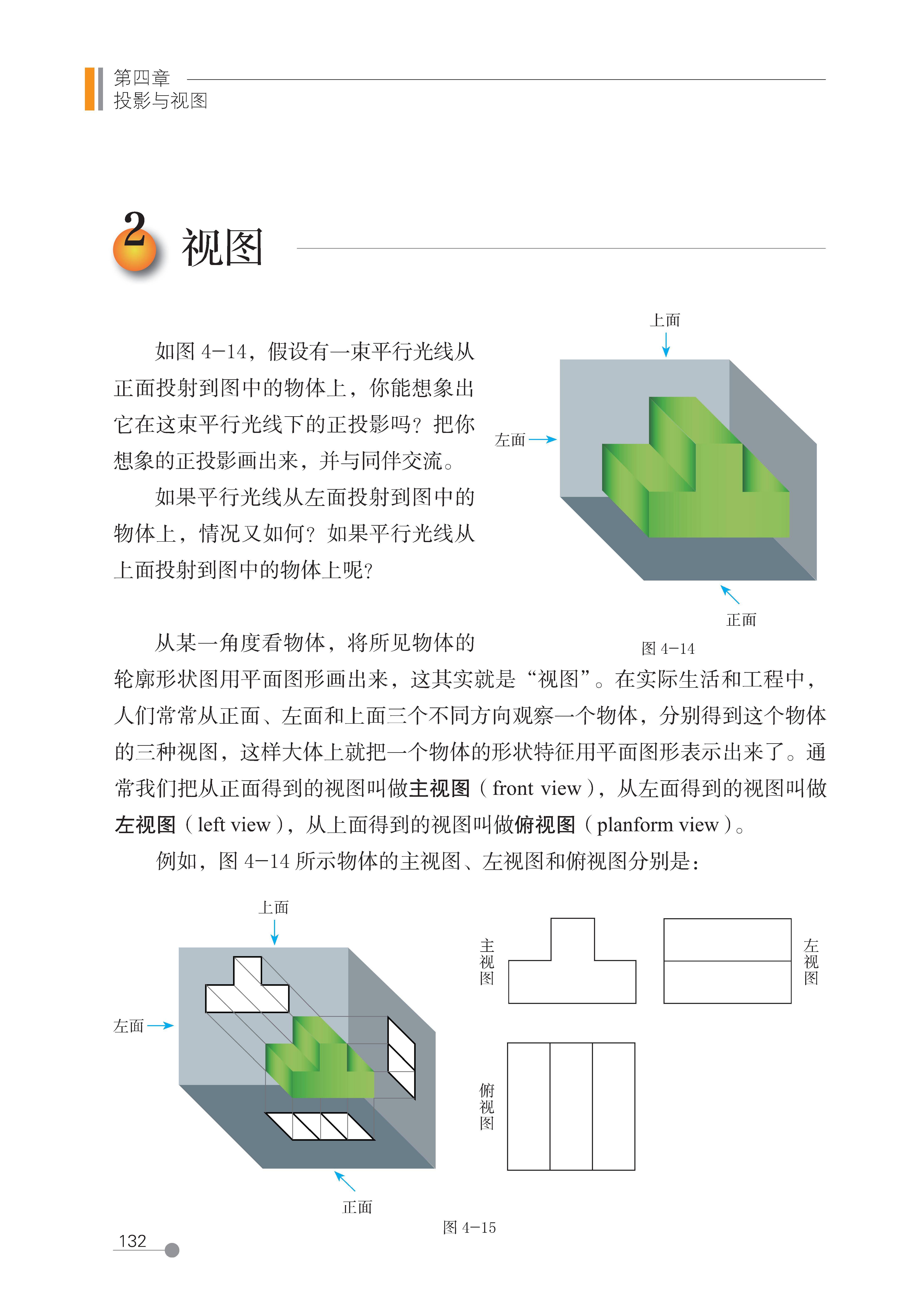
三个视图的定义（从三个固定视角观察立体图形得到的正投影）：

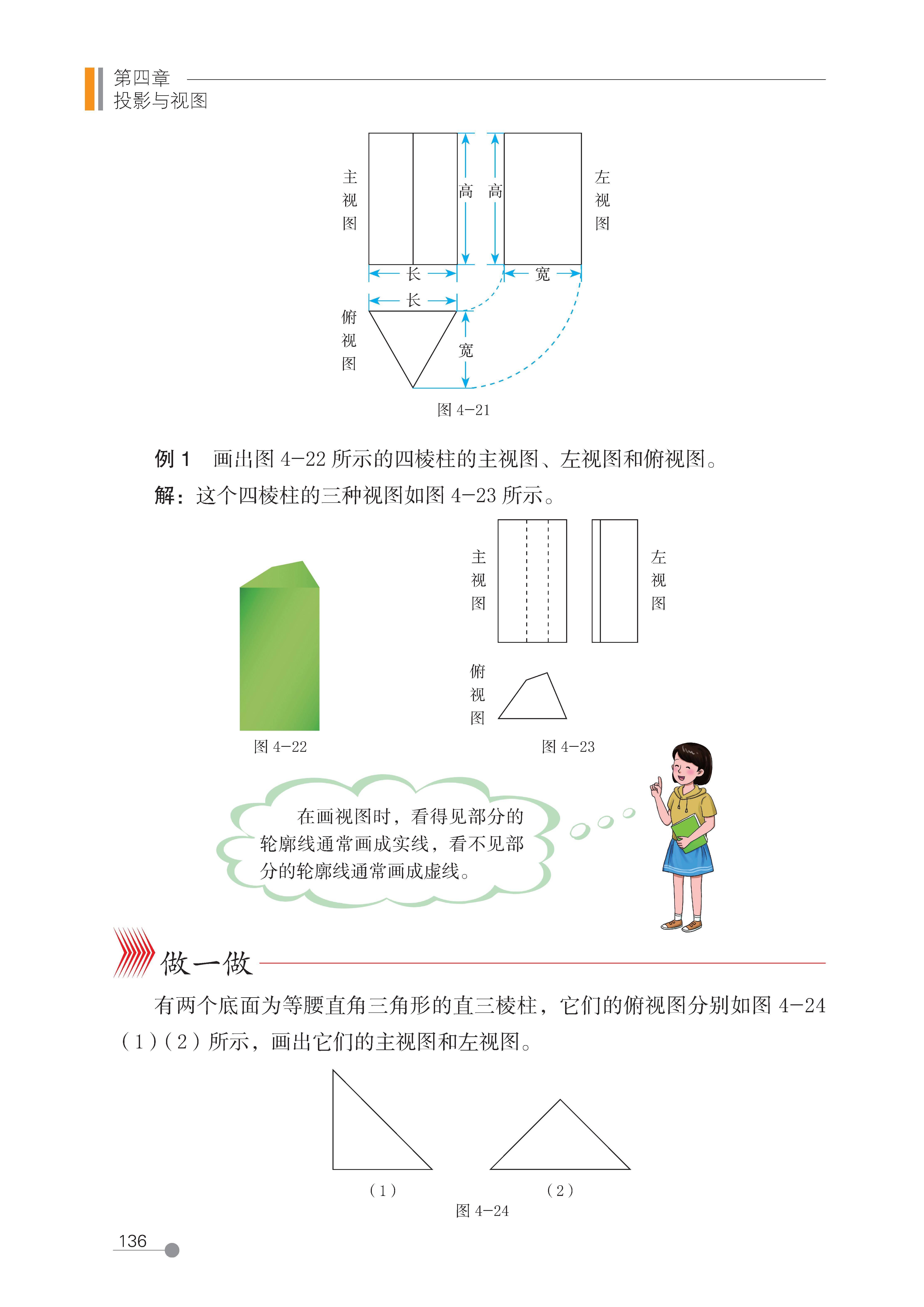
主视图：从物体的正面向后面投射得到的视图（反映物体的长和高）；

俯视图：从物体的上面向下面投射得到的视图（反映物体的长和宽）；

左视图：从物体的左面向右面投射得到的视图（反映物体的宽和高）。

三视图的摆放规则（中考绘图的规范要求）：

主视图在上方；

俯视图在主视图的正下方（与主视图 “长对正”—— 即水平方向的长度一致）；

左视图在主视图的正右方（与主视图 “高平齐”—— 即垂直方向的高度一致；与俯视图 “宽相等”—— 即垂直于长的方向的宽度一致）。

（记忆口诀：长对正、高平齐、宽相等）

2. 基本几何体的三视图绘制（基础技能，需熟练掌握）

核心几何体：正方体、长方体、圆柱、圆锥、球、棱柱（如三棱柱、四棱柱）、棱锥（如三棱锥）。

绘制重点（需注意 “看不见的棱” 的表示）：

看得见的棱、轮廓线用实线绘制；

看不见的棱、轮廓线用虚线绘制（避免遗漏，如长方体从正面看，后面的棱虽看不见，但需用虚线表示）；

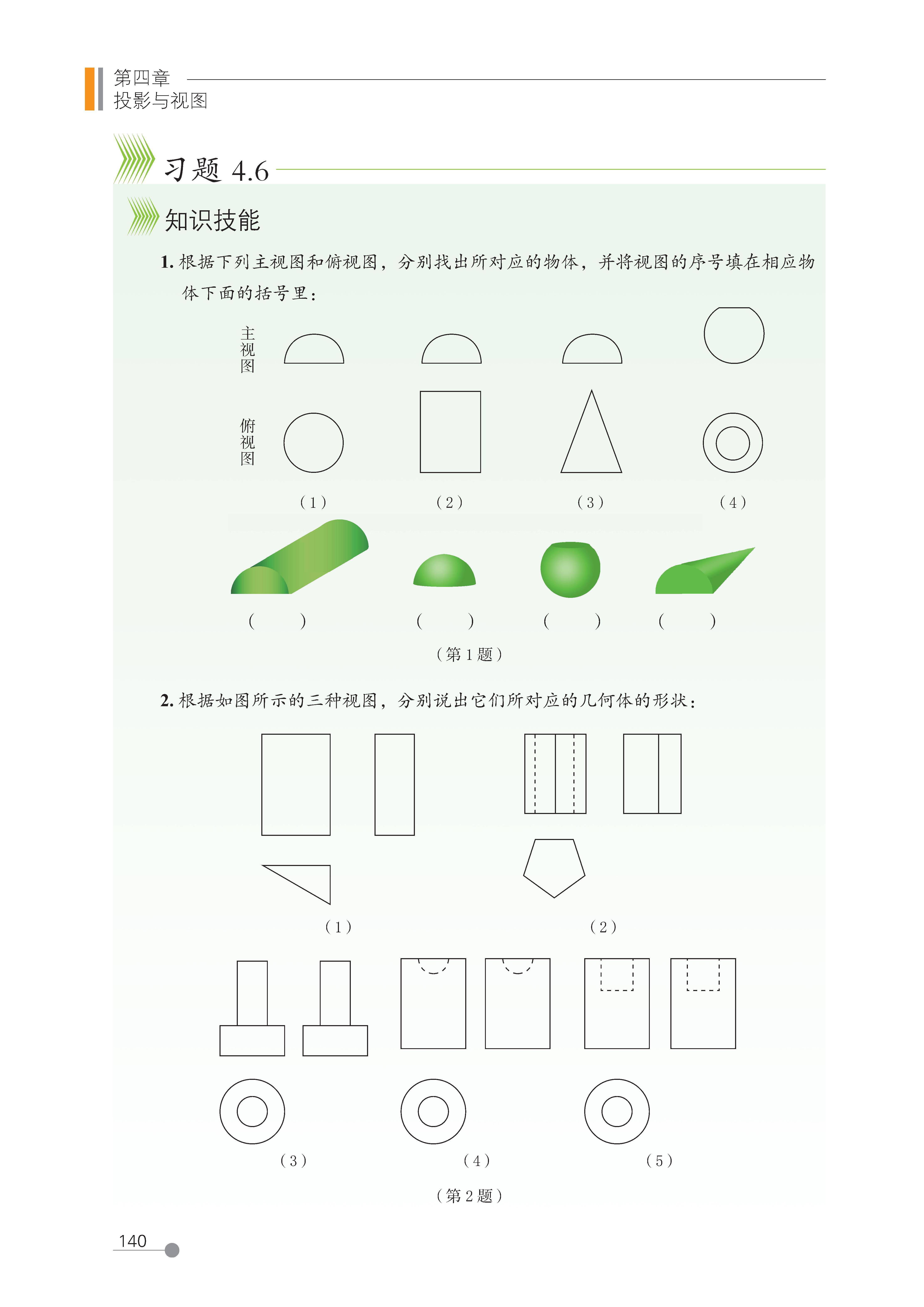
特殊几何体的三视图特征：

圆柱：主视图和左视图是 “矩形”，俯视图是 “圆”；

圆锥：主视图和左视图是 “等腰三角形”，俯视图是 “圆 + 圆心点”（圆心点表示圆锥的顶点投影）；

球：三个视图都是 “圆”（大小相同）。

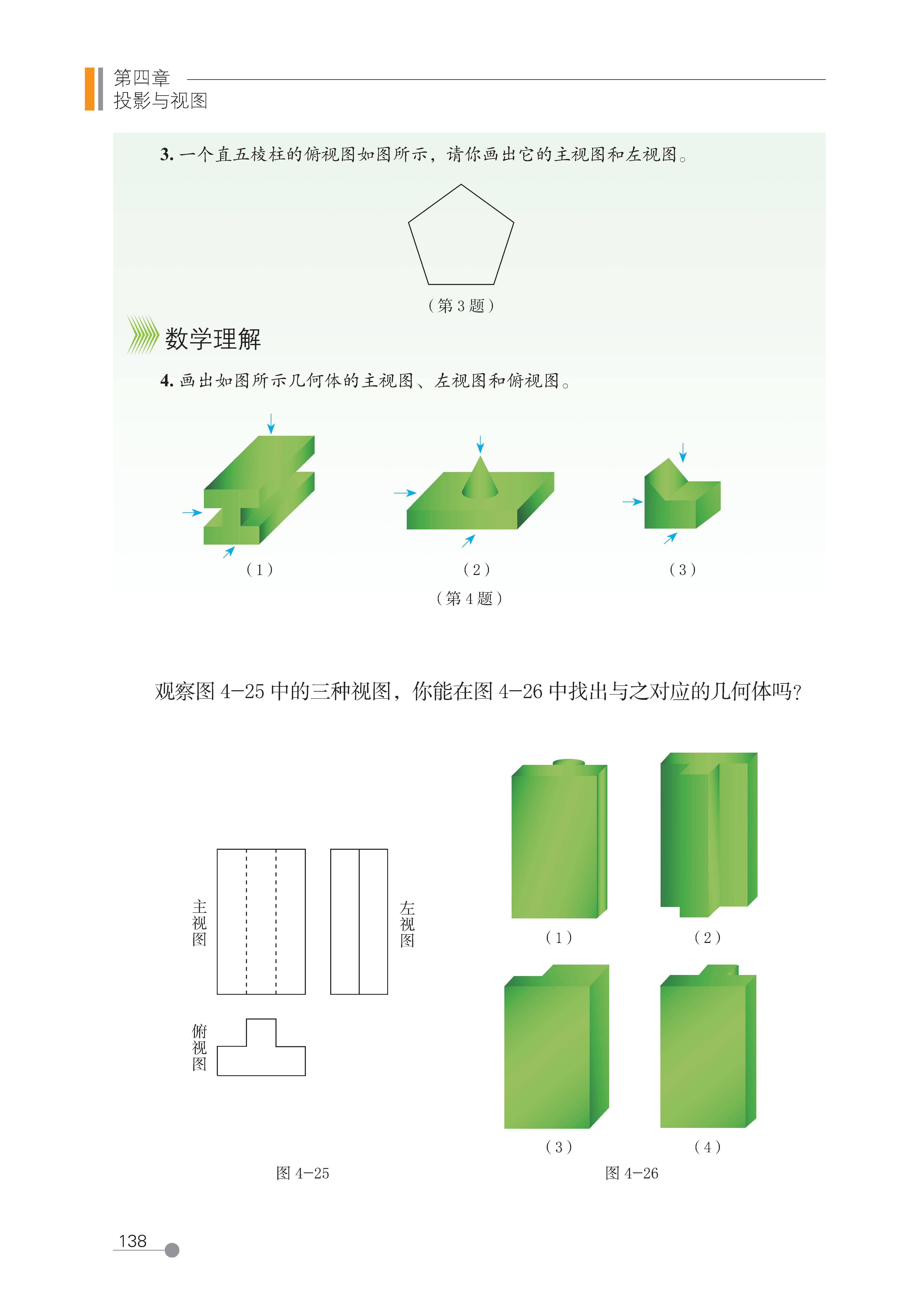
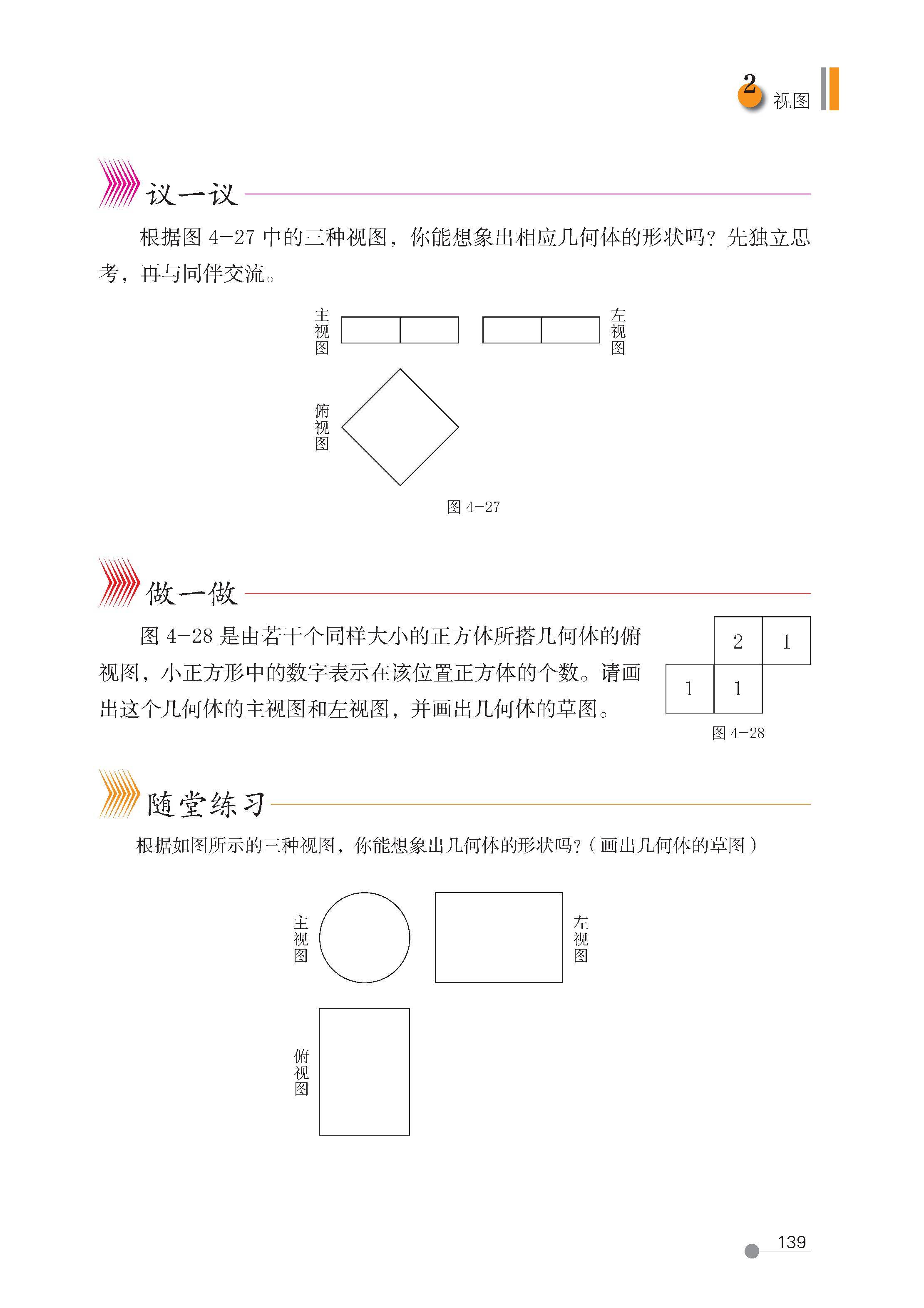
3. 由三视图还原立体图形（空间想象能力的核心考查点）

核心思路：根据 “长对正、高平齐、宽相等” 的规则，将三个视图的信息整合，还原立体图形的形状和尺寸，步骤为：

从主视图判断立体图形的 “正面形状”（如是否为柱体、锥体，有几层）；

结合俯视图判断 “底面形状”（如是否为正方形、圆形，是否有凹陷或凸起）；

用左视图验证 “侧面形状”，补充主视图和俯视图未体现的细节（如宽度方向的尺寸）；

典型题型：给出三视图，判断对应的立体图形（如 “主视图和左视图是矩形，俯视图是圆”→ 圆柱）；或根据三视图描述立体图形的组成（如由几个小正方体堆叠而成）。

4. 视图与几何体的尺寸计算（结合计算的综合考点）

核心考查：根据三视图中标注的尺寸，计算立体图形的体积或表面积（需注意 “视图尺寸与几何体实际尺寸的对应关系”）。

常见类型：

长方体：主视图的 “长”= 长方体的长，“高”= 长方体的高；俯视图的 “宽”= 长方体的宽，据此确定长、宽、高，再用公式

长

宽

高

计算体积；

圆柱：俯视图的 “圆的直径”= 圆柱的底面直径，主视图的 “高”= 圆柱的高，用公式

V=πr

2

h

（

为底面半径）计算体积；

由小正方体堆叠的几何体：根据三视图确定小正方体的个数（俯视图确定底层个数，主视图和左视图确定各层的层数），再计算总个数或表面积（注意 “重叠面” 需减去）。

三、本章核心能力要求与中考考查倾向

核心能力：空间想象能力（从立体到平面、从平面还原立体）、绘图规范能力（三视图的实线 / 虚线、摆放位置）、数形结合能力（视图尺寸与几何体计算结合）；

中考倾向：多以选择题、填空题考查 “投影类型判断”“三视图识别”“由三视图还原立体图形”；以解答题考查 “三视图绘制”“结合视图计算体积 / 表面积”（常与生活中的立体物体结合，如包装盒、工件等）。

综上，第四章 “投影与视图” 的学习重点可概括为：理解两种投影的区别与应用，掌握三视图的定义、摆放规则、绘制方法，能由三视图还原立体图形，并结合视图尺寸进行计算，核心是突破 “平面与立体的转化”，提升空间想象能力。