2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025新

人教版五年级数学（上册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

如需全套电子课本PDF版，请关注公众号“桃李科普”回复：“电子课本”

人教版五年级数学（上册）电子课本在线阅读

一、数与代数（核心基础模块）

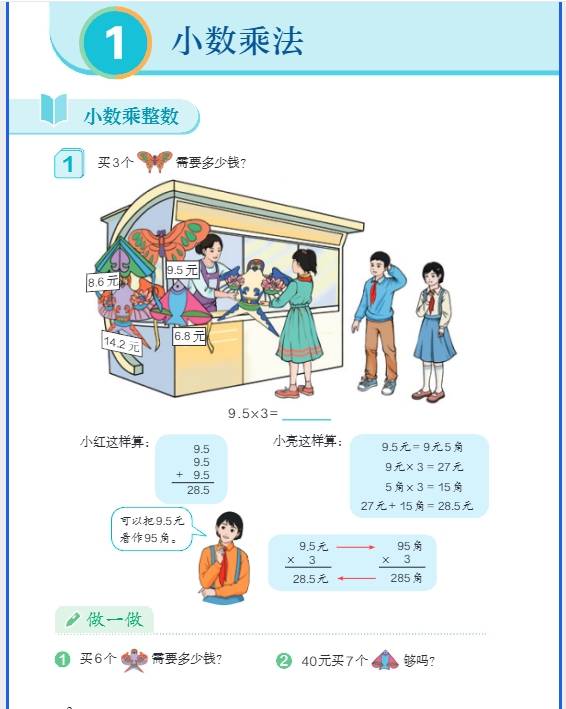
1. 小数的认识与运算

• 小数的意义：把单位 “1” 平均分成 10、100、1000…… 份，其中的 1 份或几份可以用小数表示（如 0.1 表示 1/10，0.01 表示 1/100）。
• 小数的读写：整数部分按整数读法读，小数点读 “点”，小数部分依次读每个数字（如 3.05 读作 “三点零五”）；写法需对齐小数点，空位用 0 补足。
• 小数的性质：小数末尾添上 “0” 或去掉 “0”，大小不变（如 0.6=0.60），可用于化简和改写。
• 小数的大小比较：先比整数部分，整数部分大的数大；整数部分相同，再比十分位、百分位…… 依次类推。
• 小数四则运算：
• 加减法：小数点对齐（相同数位对齐），按整数加减法计算，结果对齐小数点添上小数点。
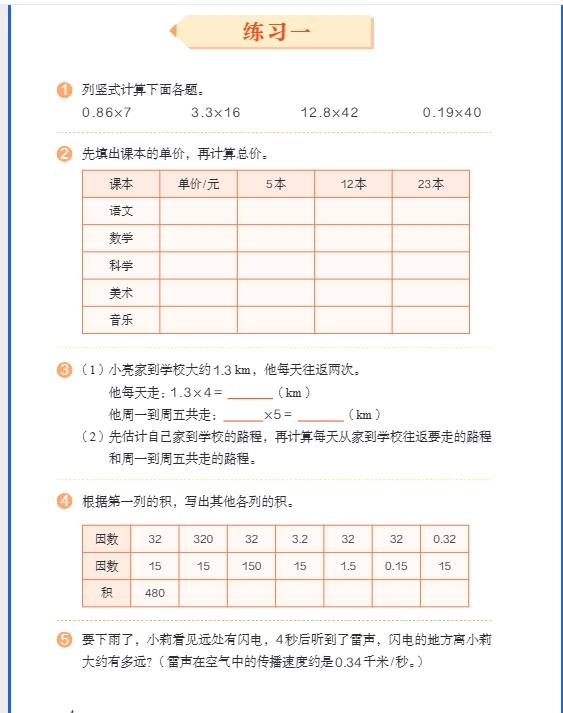
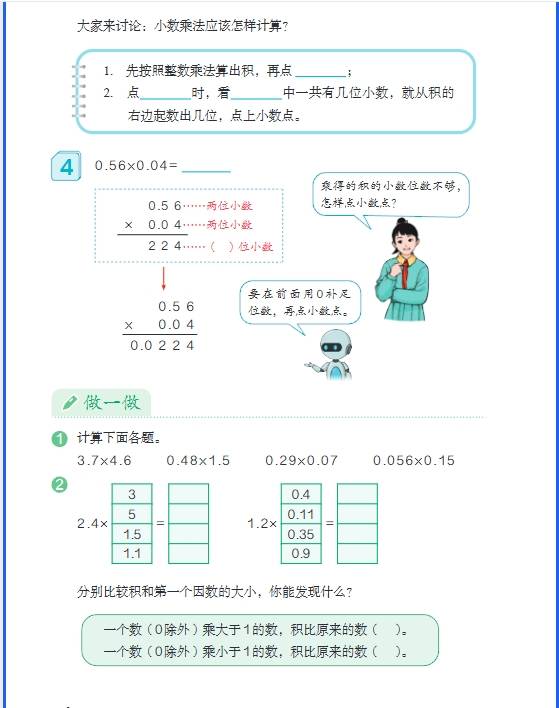
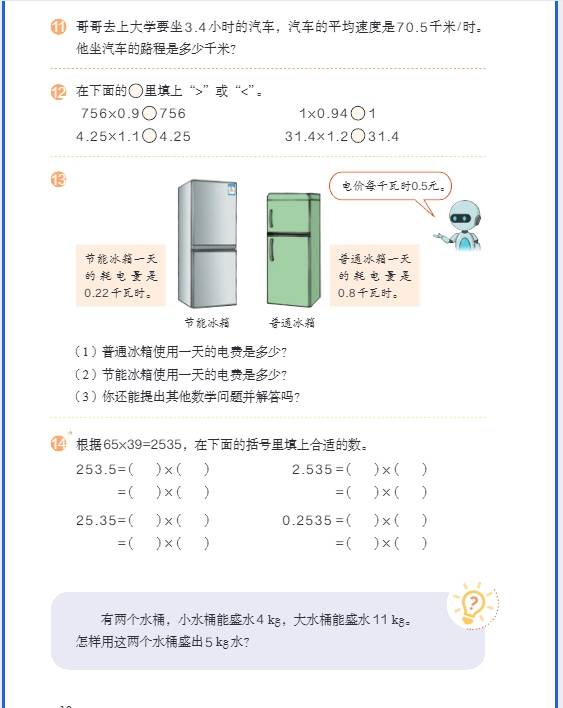
• 乘除法：乘法先按整数乘法算，再看因数共有几位小数，从积的右边起数出几位点上小数点；除法中，除数是整数时直接除，商对齐小数点；除数是小数时，先把除数化成整数（被除数同倍数扩大）再计算。

2. 分数的初步认识（下册重点）

• 分数的意义：把单位 “1” 平均分成若干份，表示这样的一份或几份的数（如 3/4 表示把单位 “1” 平均分成 4 份，取其中 3 份），分子表示取的份数，分母表示平均分的份数。
• 分数单位：把单位 “1” 平均分成若干份，其中的 1 份就是分数单位（如 5/6 的分数单位是 1/6，有 5 个这样的单位）。
• 分数的分类：真分数（分子＜分母，如 2/3）、假分数（分子≥分母，如 5/4）、带分数（整数 + 真分数，如 1 又 1/2）。
• 分数与除法的关系：被除数 ÷ 除数 = 被除数 / 除数（a÷b=a/b，b≠0），如 3÷5=3/5。
• 分数的基本性质：分数的分子和分母同时乘或除以相同的数（0 除外），分数大小不变（如 2/3=4/6=6/9），是约分和通分的基础。

3. 整数的拓展与运算

• 因数与倍数：若 a×b=c（a、b、c 为整数），则 a 和 b 是 c 的因数，c 是 a 和 b 的倍数（如 2×3=6，2 和 3 是 6 的因数，6 是 2 和 3 的倍数）。
• 2、3、5 的倍数特征：
• 2 的倍数：个位是 0、2、4、6、8（偶数）；
• 5 的倍数：个位是 0 或 5；
• 3 的倍数：各位数字之和是 3 的倍数（如 123：1+2+3=6，是 3 的倍数）。
• 质数与合数：质数（只有 1 和它本身两个因数，如 2、3、5）；合数（除 1 和本身外还有其他因数，如 4、6、8）；1 既不是质数也不是合数。
• 最大公因数与最小公倍数：通过列举法或短除法计算（如 12 和 18 的最大公因数是 6，最小公倍数是 36）。

二、图形与几何（空间想象核心）

1. 平面图形的面积

• 平行四边形的面积：公式 S = 底 × 高（S=ah），推导：通过割补法转化为长方形，长方形的长 = 平行四边形的底，宽 = 平行四边形的高。
• 三角形的面积：公式 S = 底 × 高 ÷2（S=ah÷2），推导：两个完全相同的三角形拼成一个平行四边形，面积是平行四边形的一半。
• 梯形的面积：公式 S=（上底 + 下底）× 高 ÷2（S=(a+b) h÷2），推导：两个完全相同的梯形拼成一个平行四边形，平行四边形的底 = 梯形上底 + 下底，高 = 梯形的高。
• 组合图形的面积：通过 “分割法”（分成基本图形）或 “添补法”（补成基本图形）计算，再求和或差。

2. 长方体与正方体

• 特征对比：

特征

长方体

正方体

面

6 个面，一般是长方形（相对面相等）

6 个面，都是正方形（全相等）

棱

12 条棱，相对棱长度相等

12 条棱，长度全相等

顶点

8 个

8 个

• 棱长总和：长方体 = 4×（长 + 宽 + 高）；正方体 = 12× 棱长。
• 表面积：长方体 = 2×（长 × 宽 + 长 × 高 + 宽 × 高）；正方体 = 6× 棱长 × 棱长。
• 体积：公式 V = 长 × 宽 × 高（长方体）、V = 棱长 × 棱长 × 棱长（正方体），统一公式 V = 底面积 × 高（V=Sh）。
• 体积单位：立方厘米（cm³）、立方分米（dm³）、立方米（m³），1dm³=1000cm³，1m³=1000dm³，1 升 = 1dm³，1 毫升 = 1cm³。

三、应用题与统计（综合运用模块）

1. 典型应用题

• 小数应用题：与整数应用题思路一致，需注意单位换算（如元、角、分转化）和结果保留位数（如 “够不够” 问题需估算）。
• 分数应用题：求一个数的几分之几是多少（用乘法，如 12 的 1/3 是多少：12×1/3=4）；求一个数是另一个数的几分之几（用除法，如 4 是 12 的几分之几：4÷12=1/3）。
• 行程问题：路程 = 速度 × 时间，速度 = 路程 ÷ 时间，时间 = 路程 ÷ 速度（注意相遇问题：总路程 = 速度和 × 相遇时间）。
• 工程问题：工作总量 = 工作效率 × 工作时间（常把工作总量看作单位 “1”）。

2. 统计与可能性

• 统计图：条形统计图（直观表示数量多少）、折线统计图（表示数量增减变化），需掌握读图、分析数据（求平均数、中位数）的方法。
• 可能性：用 “一定”“可能”“不可能” 描述事件发生的概率，能判断简单事件的可能性大小（如摸球游戏中，哪种颜色球多，摸到的可能性大）。

四、重点难点突破与学习方法

1. 易错点辨析：

• 小数运算：小数点对齐易错（如 3.2+0.58，需补成 3.20+0.58）；
• 面积与体积：混淆公式（如长方体表面积与体积计算，单位不同不能比较）；
• 分数与除法：忽略分母不能为 0，假分数与带分数转化错误。

1. 实用学习法：

• 具象化理解：用积木理解长方体体积，用折纸理解分数性质；
• 错题整理：按 “计算错误”“思路错误” 分类，标注错误原因；
• 生活联系：用分数表示 “切蛋糕”“分水果”，用小数计算 “购物找零”，让抽象知识具象化。