2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025新北京版六年级数学（上册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

以下是部分内容截图，完整信息请查看 PDF 文件

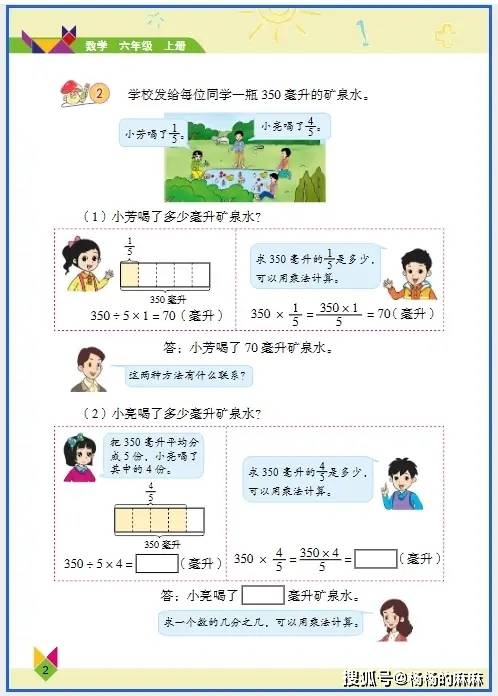
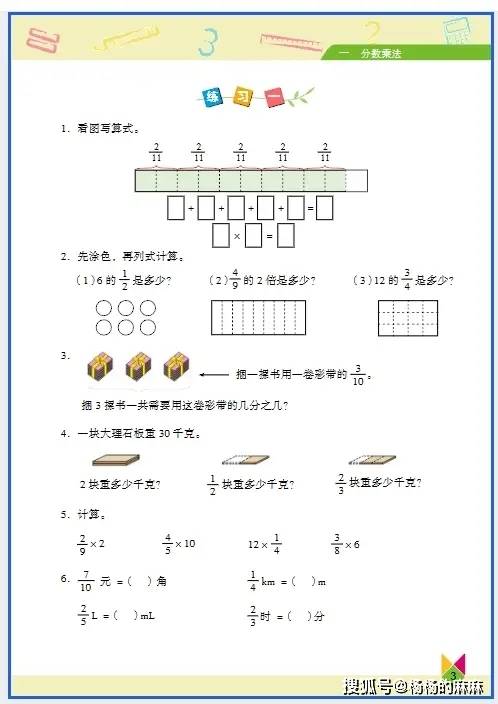
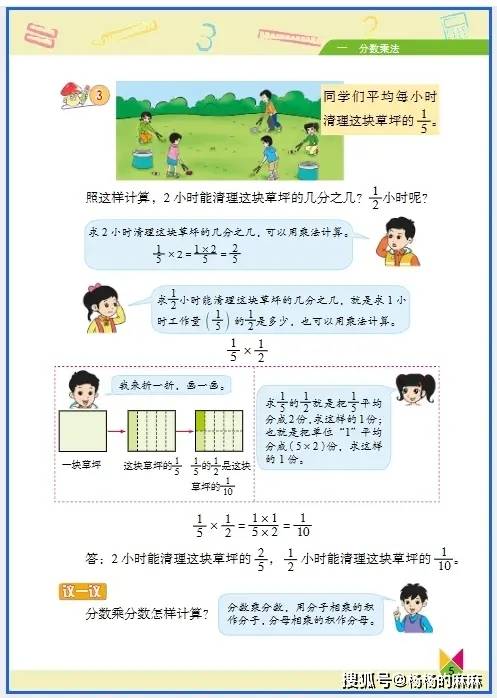
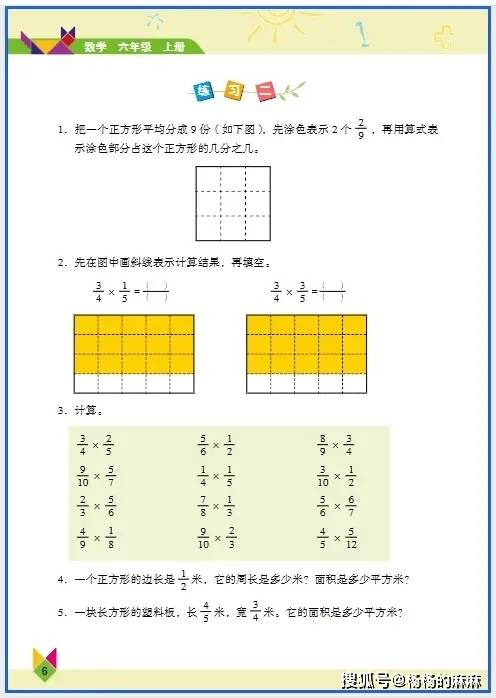
六年级数学核心知识点与趣味实践素材指南

六年级数学是小学知识体系的 “收官整合阶段”，既要实现对整数、小数、分数的综合运算贯通，又要完成从平面几何到立体几何、从具体数量到抽象比例的思维跨越，为初中数学的代数方程、几何证明奠定基础。以下从 “模块式知识点梳理”“典型误区破解”“生活化趣味实践” 三个维度，构建系统且实用的学习内容，助力学生深化理解、提升应用能力。

一、核心知识点模块梳理（附关联应用）

六年级数学围绕 “数的拓展与运算”“图形的度量与空间”“数据的分析与决策”“问题的综合解决” 四大模块展开，各模块既独立成体系，又相互关联：

（一）数的拓展与运算：从 “单一计算” 到 “关联转化”

这一模块是数学运算的 “进阶核心”，重点在于数与数之间的转化逻辑和实际场景中的灵活运用：

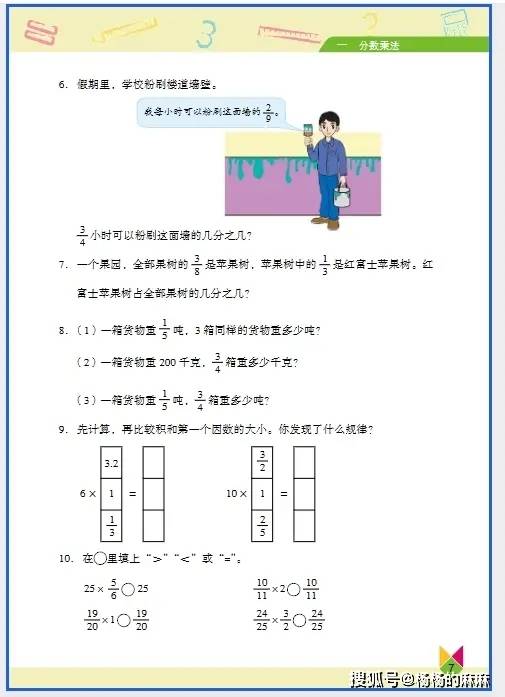
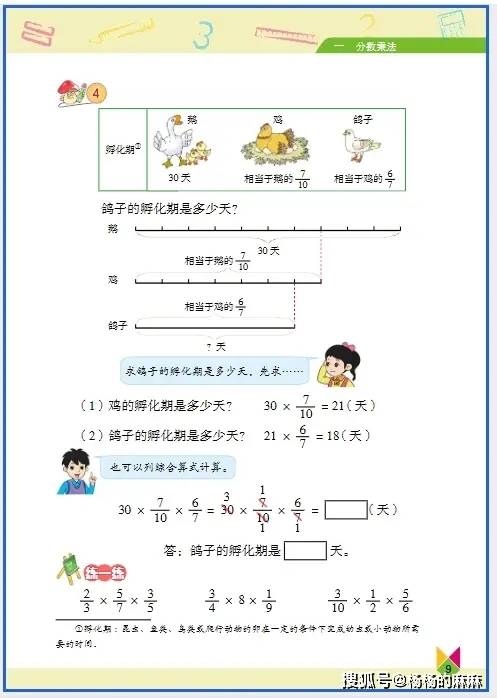
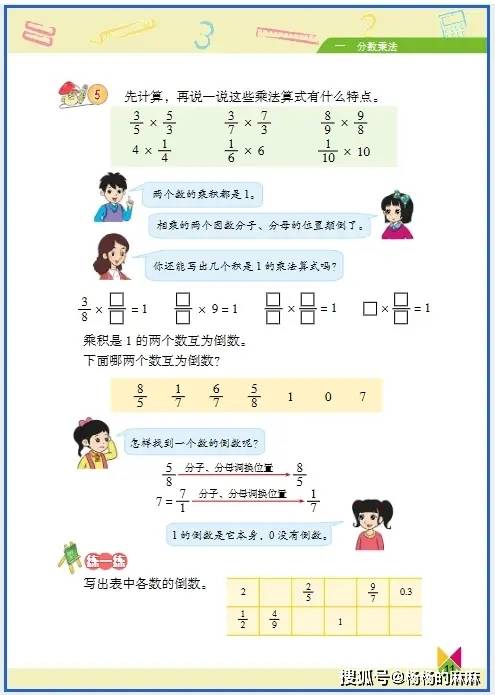
1. 分数四则运算与实际应用

• 核心逻辑：分数乘法聚焦 “求一个数的几分之几”（如 “求 24 的
• 4
• 3
• ”，本质是 “24÷4×3”）；分数除法聚焦 “已知一个数的几分之几求原数”（如 “一个数的
• 3
• 2
• 是 18，求这个数”，需用 “18÷
• 3
• 2
• =18×
• 2
• 3
• ”）；混合运算需遵循 “先乘除后加减，有括号先算括号内”，且能灵活运用运算律简算（如
• 6
• 5
• ×4
• 3
• +6
• 5
• ×4
• 1
• =6
• 5
• ×(4
• 3
• +4
• 1
• )
• ）。
• 典型应用：工程问题（“一项工程，甲队单独做 8 天完成，乙队单独做 12 天完成，两队合作几天完成？”，需先求工作效率
• 8
• 1
• 和
• 12
• 1
• ，再用 “1÷(\frac {1}{8}+\frac {1}{12})
• ”计算）；行程问题（“小明从家到学校，走了全程的
• \frac{2}{5}
• 后还剩600米，全程多少米？”，用“600÷(1−5
• 2
• )
• ” 求解）。

2. 百分数的多维应用

• 核心逻辑：百分数是 “分母为 100 的特殊分数”，重点掌握 “三重转化”（小数化百分数：小数点右移两位加 %；分数化百分数：先化成小数再转化；百分数化分数：去掉 % 后约分）；实际应用中需区分 “百分率”（如合格率、出勤率，反映部分与整体的比例）和 “百分比变化”（如增长率、降价幅度，反映变化量与原量的比例）。
• 典型应用：经济场景（“一台电脑原价 4000 元，先降价 10%，再涨价 10%，现价多少元？”，需分步计算：4000×(1-10%)=3600 元，3600×(1+10%)=3960 元）；浓度场景（“将 20 克盐放入 180 克水中，盐水的浓度是多少？”，用 “20÷(20+180)×100%=10%” 计算）。

3. 比与比例的深层理解

• 核心逻辑：“比” 是两个数的倍数关系（如 3:4 表示 “3 份与 4 份的比”），需掌握 “化简比”（将比化成最简整数比，如 15:20=3:4）和 “求比值”（用前项除以后项，如 3:4=0.75）；“比例” 是两个比相等的式子（如 3:4=6:8），利用 “内项积 = 外项积” 解比例（如 3:x=6:8，x=4）；正反比例需紧扣 “变量关系”—— 正比例是 “比值一定”（如 “速度不变，路程与时间”），反比例是 “乘积一定”（如 “路程不变，速度与时间”）。
• 典型应用：按比例分配（“将 60 颗糖果按 2:3 分给甲、乙两人，甲得多少颗？”，先算总份数 2+3=5，甲占
• 5
• 2
• ，60×
• 5
• 2
• =24 颗）；比例尺应用（“地图比例尺 1:10000，图上距离 2 厘米，实际距离多少米？”，2×10000=20000 厘米 = 200 米）。

4. 负数的初步认知与应用

• 核心逻辑：负数是 “表示相反意义的量”，需明确 “0 既不是正数也不是负数”，在数轴上 “从左到右数逐渐增大”（如 - 5＜-2＜0＜3）；生活中常用负数表示 “低于基准” 的量（如零下温度、海拔负数、支出金额）。
• 典型应用：温度对比（“北京气温 - 3℃，上海气温 5℃，两地温差多少？”，5-(-3)=8℃）；财务记录（“小明本月零花钱收入 100 元记为 + 100 元，买文具花 25 元记为 - 25 元，月末结余多少？”，100-25=75 元）。

（二）图形与几何：从 “平面度量” 到 “立体计算”

这一模块是空间思维的 “关键突破点”，重点在于掌握图形的特征、公式推导及实际场景中的度量计算：

1. 圆的深度认知与应用

• 核心逻辑：圆的 “两大要素”—— 圆心（O，确定位置）、半径（r，确定大小），直径 d=2r；周长推导需理解 “π 是周长与直径的比值”（C=πd 或 C=2πr）；面积推导需掌握 “化圆为方” 思想（将圆分割成扇形拼成长方形，长方形长 =πr、宽 = r，故 S=πr²）。
• 典型应用：组合图形计算（“一个正方形边长 10 厘米，内部画一个最大的圆，圆的面积是多少？”，圆直径 = 正方形边长 = 10 厘米，r=5 厘米，S=3.14×5²=78.5 平方厘米）；实际场景（“给直径 1 米的圆形餐桌铺桌布，桌布边缘下垂 20 厘米，桌布面积多少？”，桌布直径 = 1+0.2×2=1.4 米，r=0.7 米，S=3.14×0.7²=1.5386 平方米）。

2. 圆柱与圆锥的表面积、体积计算

• 核心逻辑：圆柱 “两底一侧”—— 底面积 S 底 =πr²，侧面积 S 侧 = 底面周长 × 高 = 2πrh，表面积 S 表 = 2S 底 + S 侧（无盖时 S 表 = S 底 + S 侧）；体积推导需关联 “长方体体积”（将圆柱切拼成长方体，V=S 底 ×h=πr²h）。圆锥 “一底一侧”—— 体积是 “等底等高圆柱体积的
• 3
• 1
• ”（V=
• 3
• 1
• πr²h），需强调 “等底等高” 是前提条件。
• 典型应用：圆柱场景（“做一个底面半径 2 分米、高 5 分米的无盖水桶，需多少铁皮？能装多少水？”，铁皮面积 = 3.14×2²+2×3.14×2×5=75.36 平方分米；容积 = 3.14×2²×5=62.8 立方分米 = 62.8 升）；圆锥场景（“一个圆锥形沙堆，底面周长 12.56 米，高 1.5 米，每立方米沙重 1.6 吨，沙堆总重多少？”，r=12.56÷3.14÷2=2 米，V=
• 3
• 1
• ×3.14×2²×1.5=6.28 立方米，总重 = 6.28×1.6=10.048 吨）。

（三）数据的分析与决策：从 “数据呈现” 到 “信息提取”

这一模块聚焦 “数据的解读与运用”，重点在于根据需求选择合适的统计图，并从数据中提取有效信息：

1. 统计图的选择与分析

• 核心逻辑：条形统计图 “直观对比数量多少”（如 “各班人数对比”）；折线统计图 “反映数据变化趋势”（如 “一周气温变化”）；扇形统计图 “体现部分与整体关系”（如 “家庭支出占比”）。分析时需关注 “数据单位”“图例含义”“特殊数据节点”（如折线图中的峰值、谷值）。
• 典型应用：扇形统计图分析（“某家庭每月支出扇形图中，食品支出占 30%，教育支出占 25%，已知食品支出比教育支出多 500 元，家庭月总支出多少？”，500÷(30%-25%)=10000 元）；折线统计图预测（“某商店上半年销售额折线图显示每月增长 2000 元，6 月销售额 15000 元，预测 7 月销售额多少？”，15000+2000=17000 元）。

2. 概率的初步探索

• 核心逻辑：简单随机事件的 “可能性大小”（如抛硬币正面朝上概率
• 2
• 1
• ，摸红球概率 = 红球数量 ÷ 总球数），需区分 “确定事件”（如 “太阳从东方升起”，概率 1）和 “不确定事件”（如 “明天会下雨”，概率 0-1 之间）。
• 典型应用：游戏公平性判断（“一个袋子里有 3 个红球、1 个白球，摸到红球甲赢，摸到白球乙赢，游戏公平吗？”，甲赢概率
• 4
• 3
• ，乙赢概率
• 4
• 1
• ，不公平，需增加 2 个白球使红、白球数量相等）。

（四）问题的综合解决：跨模块知识融合

这一模块是数学能力的 “综合体现”，需整合数与代数、图形与几何知识，解决复杂实际问题：

• 典型类型：鸡兔同笼问题（“鸡兔共 20 只，脚 56 只，鸡兔各多少只？”，用方程法：设鸡 x 只，兔 (20-x) 只，2x+4 (20-x)=56，解得 x=12，兔 8 只）；行程相遇问题（“甲、乙两车从相距 360 千米的两地相向而行，甲速 60 千米 / 时，乙速 40 千米 / 时，几小时后相遇？”，相遇时间 = 总路程 ÷ 速度和 = 360÷(60+40)=3.6 小时）。

二、典型误区破解（附实用避坑策略）

六年级数学的误区多源于 “概念理解不透彻”“细节关注不到位”“场景分析不全面”，以下针对高频误区给出具体破解方法：

1. 分数应用：“分率” 与 “具体量” 混淆

• 误区示例：“一根 10 米长的绳子，第一次剪去
• 5
• 1
• ，第二次剪去
• 5
• 1
• 米，两次共剪去多少米？” 错算为 “10×
• 5
• 1
• ×2=4 米”（正确：第一次剪去 10×
• 5
• 1
• =2 米，两次共剪 2+
• 5
• 1
• =2.2 米）。
• 避坑策略：关键看 “分数后是否带单位”—— 带单位（如
• 5
• 1
• 米）是 “具体量”，直接用数值计算；不带单位（如
• 5
• 1
• ）是 “分率”，需先乘单位 “1” 的量（如绳子总长）得到具体量，再进一步计算。

2. 圆柱表面积：“场景需求” 与 “公式匹配” 错位

• 误区示例：“做一节长 1 米、底面直径 20 厘米的通风管，需多少铁皮？” 错算为 “2×3.14×10²+2×3.14×10×100=6908 平方厘米”（正确：通风管无底面，只需算侧面积，2×3.14×10×100=6280 平方厘米）。
• 避坑策略：先判断 “物体是否需要底面” 及 “需要几个底面”—— 通风管、烟囱 “无底面”，只算侧面积；水桶、鱼缸 “1 个底面”，算侧面积 + 1 个底面积；罐头盒、圆柱礼盒 “2 个底面”，算侧面积 + 2 个底面积，再统一单位进行计算。

3. 比例判断：“变量关系” 分析不精准

• 误区示例：“正方形的面积与边长” 错判为正比例关系（正确：面积 = 边长 × 边长，面积与边长的比值 “边长” 是变化的，不成正比例；面积与边长的平方成正比例）。
• 避坑策略：按 “三步法” 判断 —— 第一步，写出两个变量的关系式（如面积 S = 边长 a×a）；第二步，看关系式是否符合 “正比例（
• x
• y
• =k
• ，k 为定值）” 或 “反比例（x×y=k，k 为定值）”；第三步，验证比值或乘积是否为定值（如 S 与 a 的比值是 a，不是定值，故不成正比例）。

4. 百分数变化：“单位 1” 切换不清晰

• 误区示例：“某商品先涨价 20%，再降价 20%，现价与原价相等吗？” 错认为 “相等”（正确：设原价 100 元，涨价后 100×(1+20%)=120 元，降价后 120×(1-20%)=96 元，现价低于原价）。
• 避坑策略：每次价格变化的 “单位 1” 不同 —— 涨价时 “单位 1 是原价”，降价时 “单位 1 是涨价后的价格”，需分步计算，且不能直接用 “涨价幅度 - 降价幅度” 判断最终价格变化。

三、趣味实践素材（生活化、可操作）

通过 “动手实践” 将抽象知识转化为直观体验，既能提升学习兴趣，又能深化知识理解：

1. 家庭理财小管家（百分数应用）

• 实践任务：记录家庭一周的收支情况（收入记为正数，支出记为负数），计算 “每日结余” 和 “一周总结余”；选择一笔支出（如买菜花费 80 元），分析其中 “蔬菜、肉类、水果” 的占比，用扇形统计图呈现，并计算 “肉类支出比蔬菜多百分之几”。
• 能力提升：掌握负数的实际应用、百分数的占比计算，培养数据整理与分析能力。

2. 圆柱圆锥手工制作（立体几何应用）计算，培养数据整理与分析能力。

2. 圆柱圆锥手工制作（立体几何应用）

• 实践任务：用硬纸板制作一个 “无盖圆柱笔筒”（先测量确定底面半径和高，如 r=3 厘米，h=10 厘米，计算所需硬纸板面积：3.14×3²+2×3.14×3×10=216.66 平方厘米，再裁剪粘贴）；用橡皮泥制作 “等底等高的圆柱和圆锥