26春人教版七年级下册数学电子课本教科书【高清教材】可打印
今天为大家分享:人教版七年级下册数学教材,以 “几何直观 + 代数建模” 为核心,通过 “相交线与平行线 — 实数 — 平面直角坐标系 — 二元一次方程组 — 不等式与不等式组 — 数据的收集、整理与描述” 的递进结构,为学生搭建了从直观几何到抽象代数的完整知识体系,是七年级学生深化数学认知、培养核心素养的核心载体。

以下为部分截图,请获取完整的P.D.F









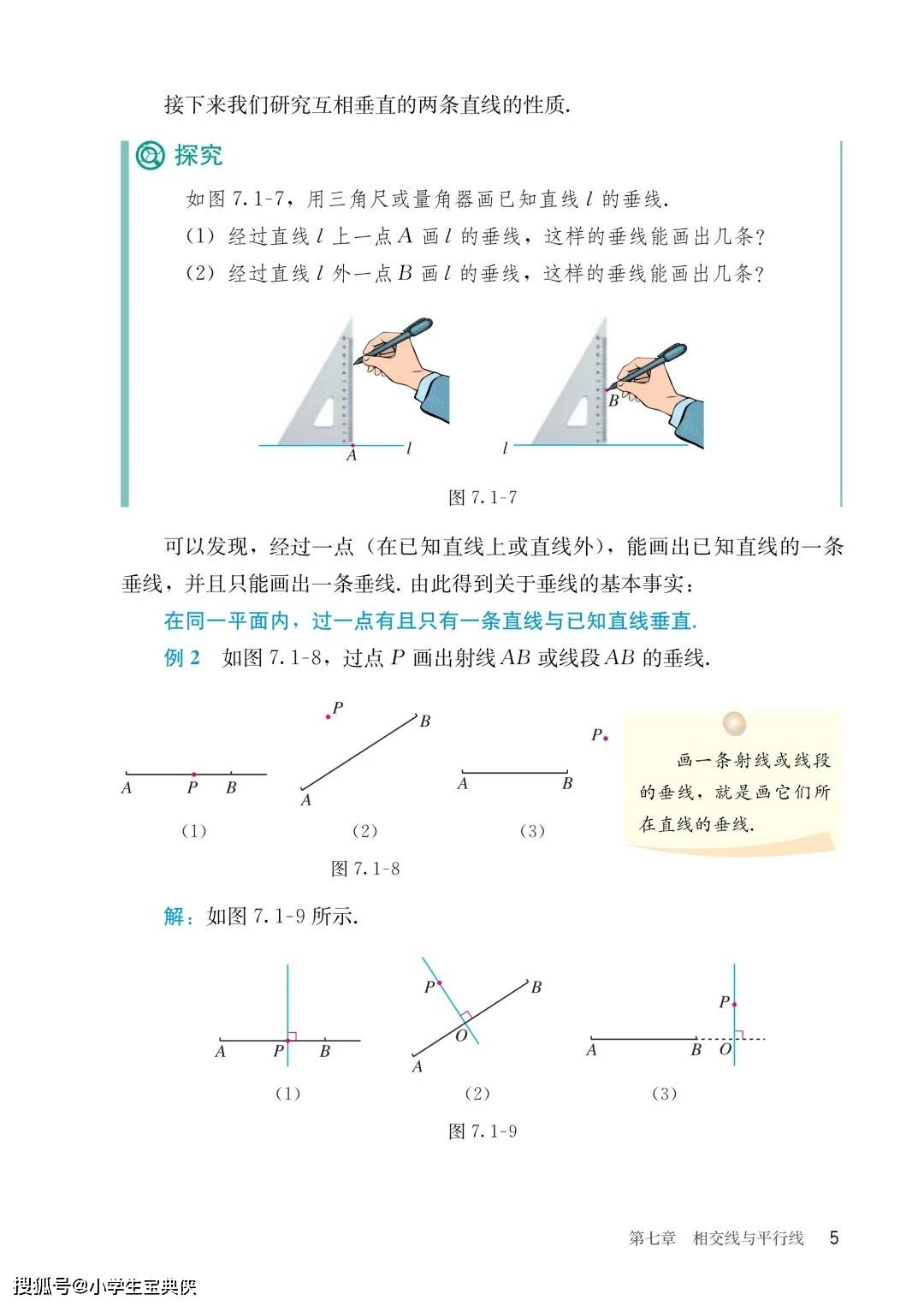


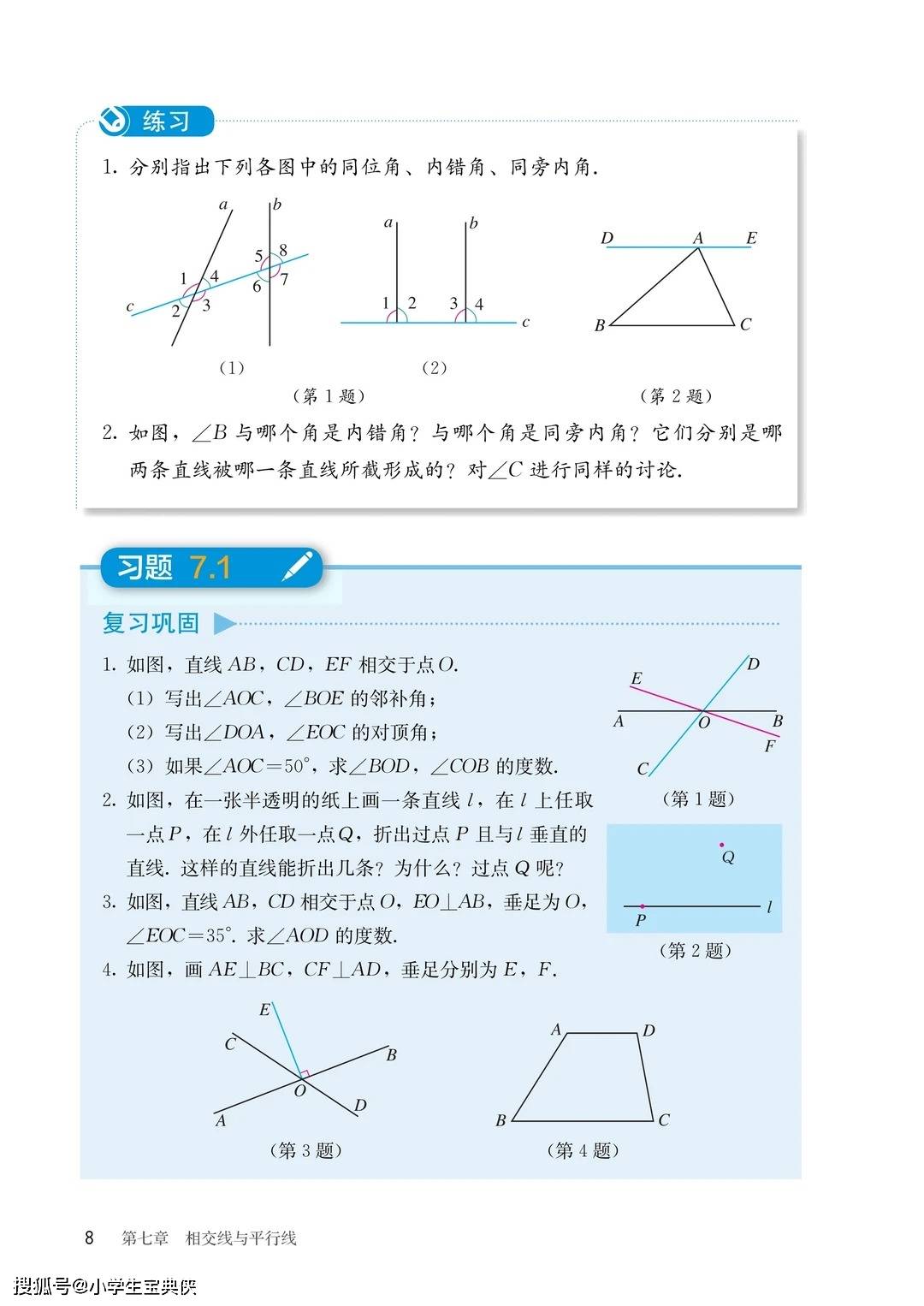
教材开篇以桥梁、公路等生活场景切入,从相交线的对顶角、邻补角性质,到平行线的判定与性质,再到图形的平移,引导学生通过直观想象、操作确认、推理论证等方法,初步体会严谨的几何推理,培养 “言之有据” 的思考习惯。这不仅为后续三角形、四边形的学习筑牢基础,更能让学生理解 “数学结论需要逻辑支撑” 的学科本质。
随后,教材将数的范围从有理数扩展到实数,通过平方根、立方根的学习,让学生认识无理数的存在,体会实数与数轴上点的一一对应关系,完成从 “有限” 到 “无限” 的认知突破。平面直角坐标系的引入,则建立了 “点与有序数对” 的关联,让学生能用代数方法研究几何图形,也能用几何图形表示代数结果,实现 “数形结合” 的思维跨越。
在代数模块,教材通过二元一次方程组、不等式与不等式组的学习,引导学生建立数学模型解决实际问题。从 “消元法” 解方程组,到不等式的性质与解法,再到利用统计图表描述数据,让学生逐步提升抽象能力、运算能力与应用意识。教材还融入 “低碳生活”“白昼时长规律的探究” 等综合实践活动,让学生在解决真实问题的过程中,理解数学与生活的紧密联系。
教材的亮点在于 “思维驱动 + 素养导向” 的设计理念。每节课都配套 “探究”“思考”“练习” 等环节,比如通过转动木条的模型探究对顶角的性质,用数轴直观展示实数的连续性。这些设计不仅让学生在操作中深化对知识的理解,更能培养观察分析、归纳推理的科学思维。同时,教材穿插 “阅读与思考”“探究与发现” 等拓展板块,介绍 “为什么√2 不是有理数”“用求差法比较大小” 等内容,拓宽学生的数学视野。
对七年级学生来说,这套教材不仅是应对考试的工具,更是培养数学思维的载体。它让学生从 “记忆公式” 走向 “理解本质”,从 “被动解题” 走向 “主动建模”,为高中数学学习和未来的逻辑思维培养筑牢坚实基础。
