26春新教材|人教版|五年级下册数学电子课本(pdf可打印)
今天为大家分享:人教版五年级下册数学教材主要包含十个部分,分别是观察物体(三)、因数和倍数、长方体和正方体、探索图形、分数的意义和性质、图形的运动(三)、分数的加法和减法、折线统计图、数学广角 —— 找次品以及总复习。这些内容围绕空间与图形、数与代数、统计与概率以及数学思考四个领域展开,构成了五年级下学期的数学学习框架。

以下为部分截图,请获取完整的P.D.F



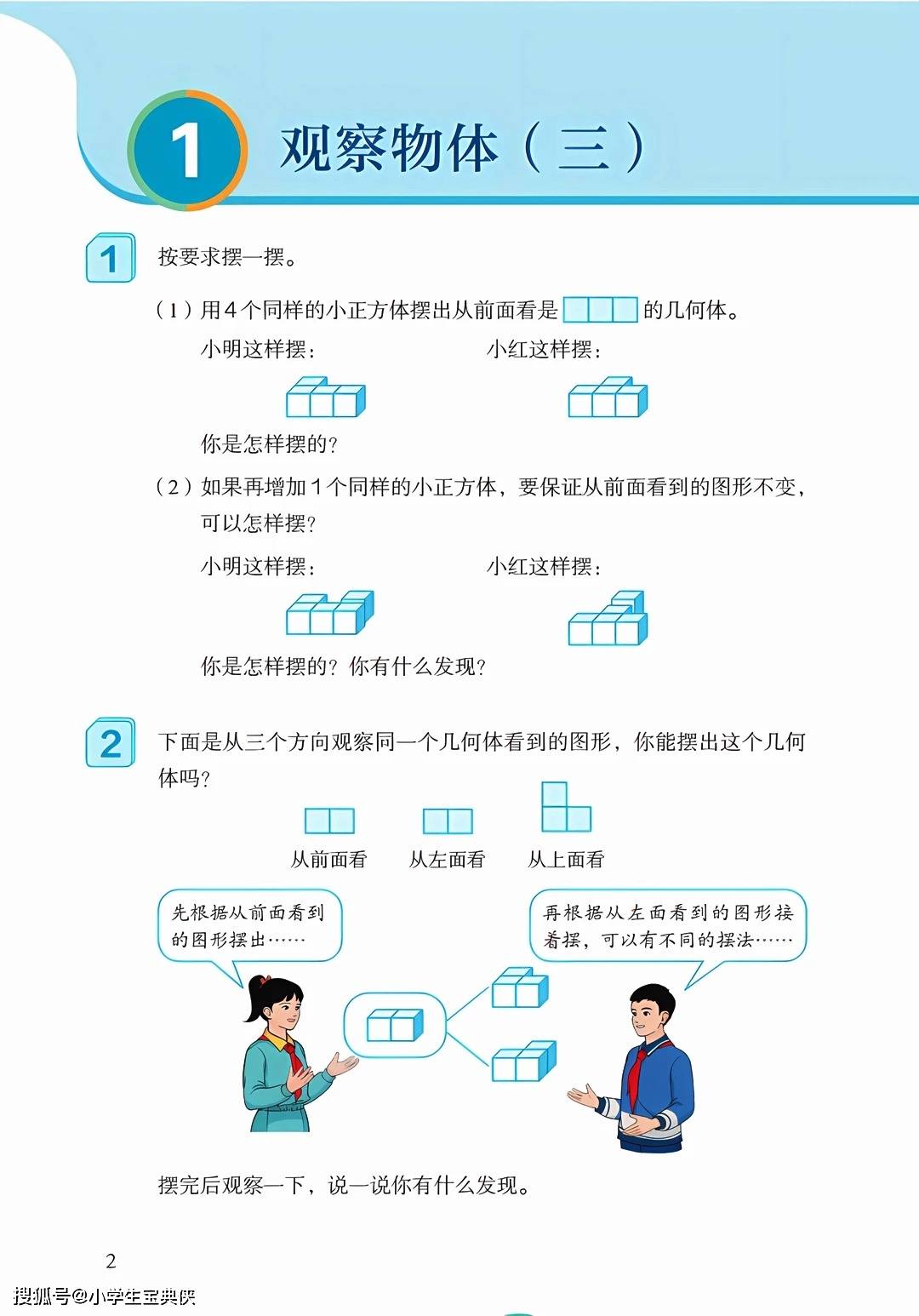
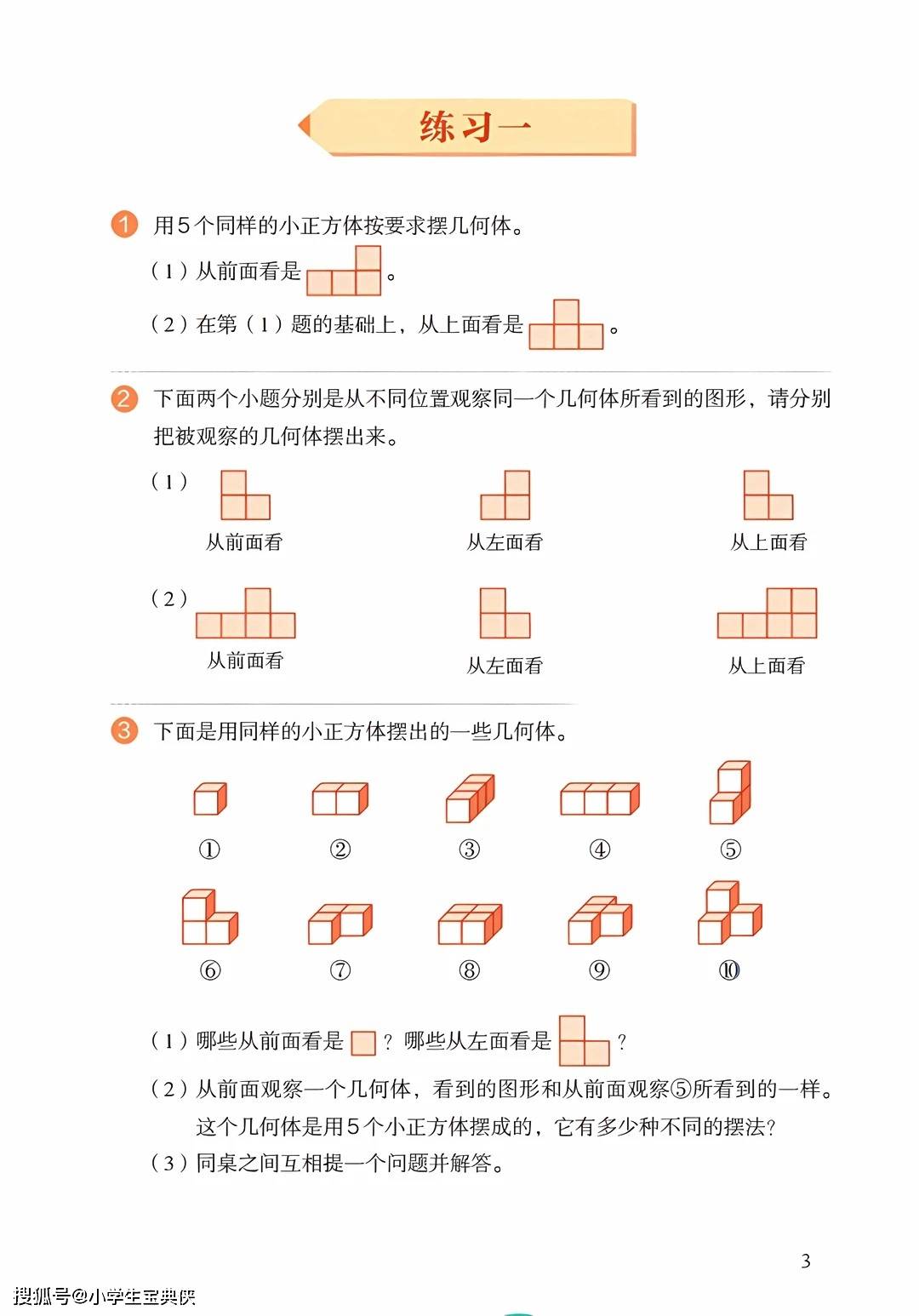
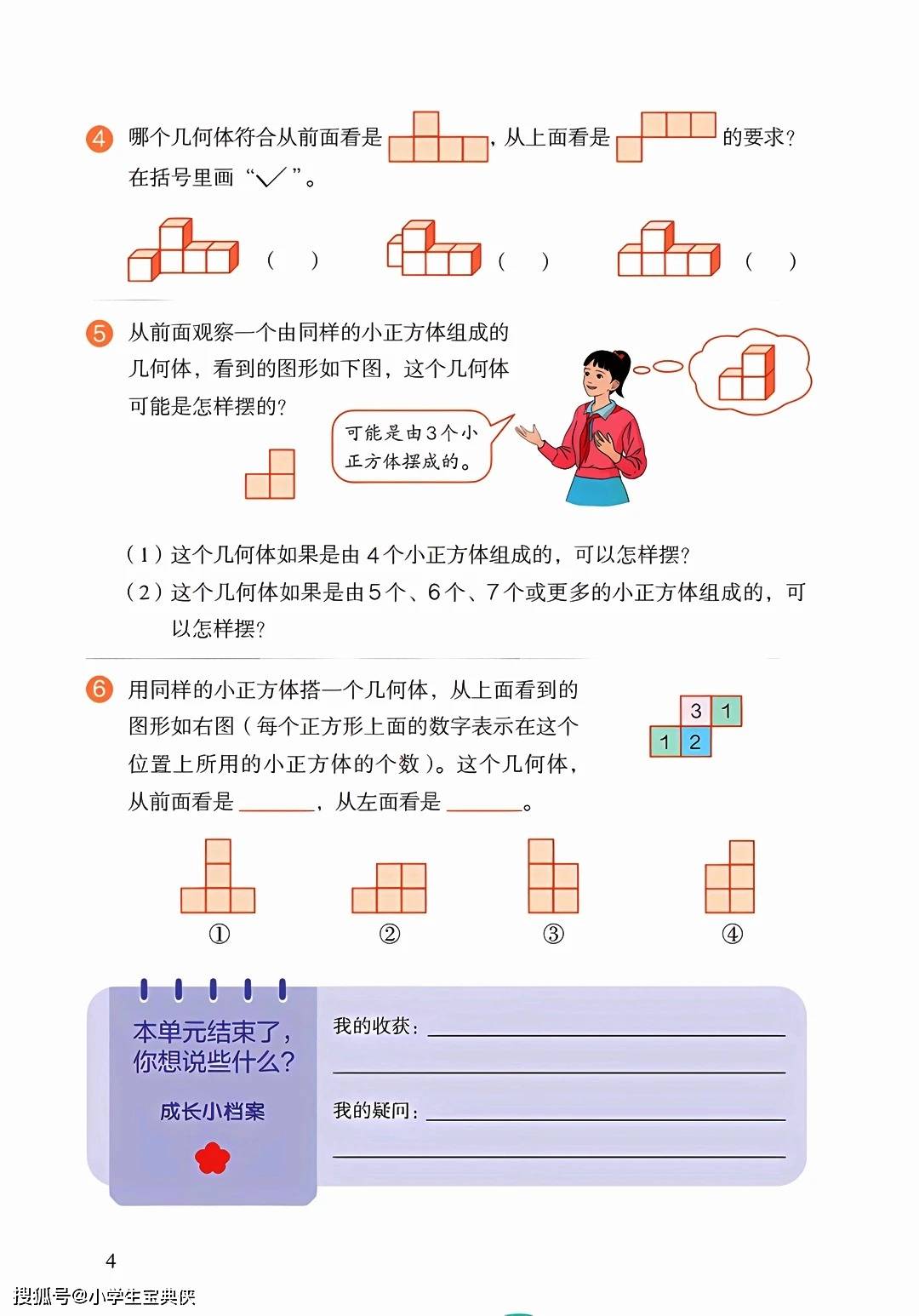






在观察物体(三)部分,学生主要学习根据从不同方向看到的平面图形来还原立体图形。通过从前面、上面、左面三个方向的观察结果,可以推断出小正方体的摆放方式。同一个视图可能对应多种摆法,而三个方向的视图通常能确定唯一的几何体结构。这一部分内容有助于学生建立空间想象能力,理解立体图形与平面图形之间的对应关系。
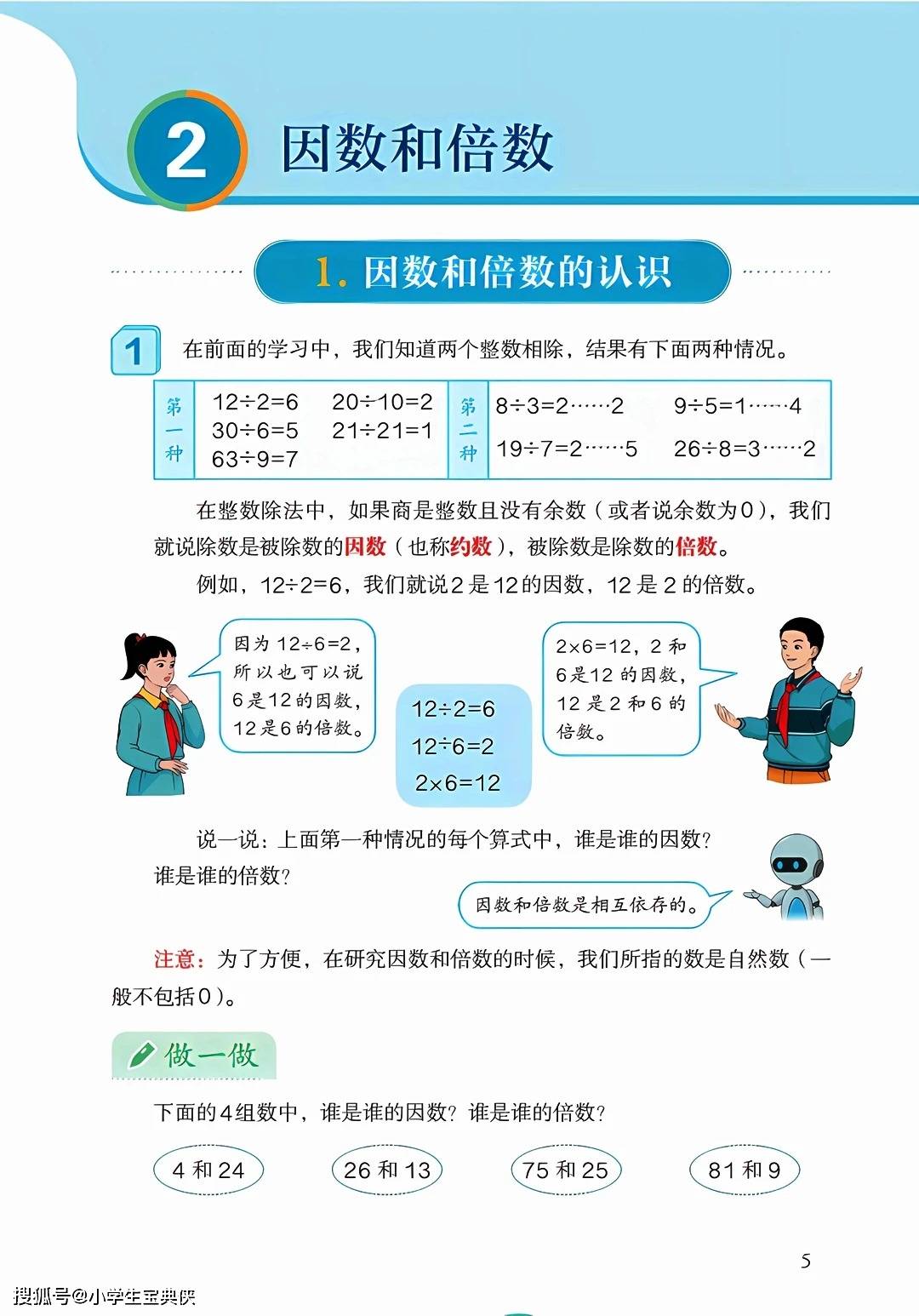
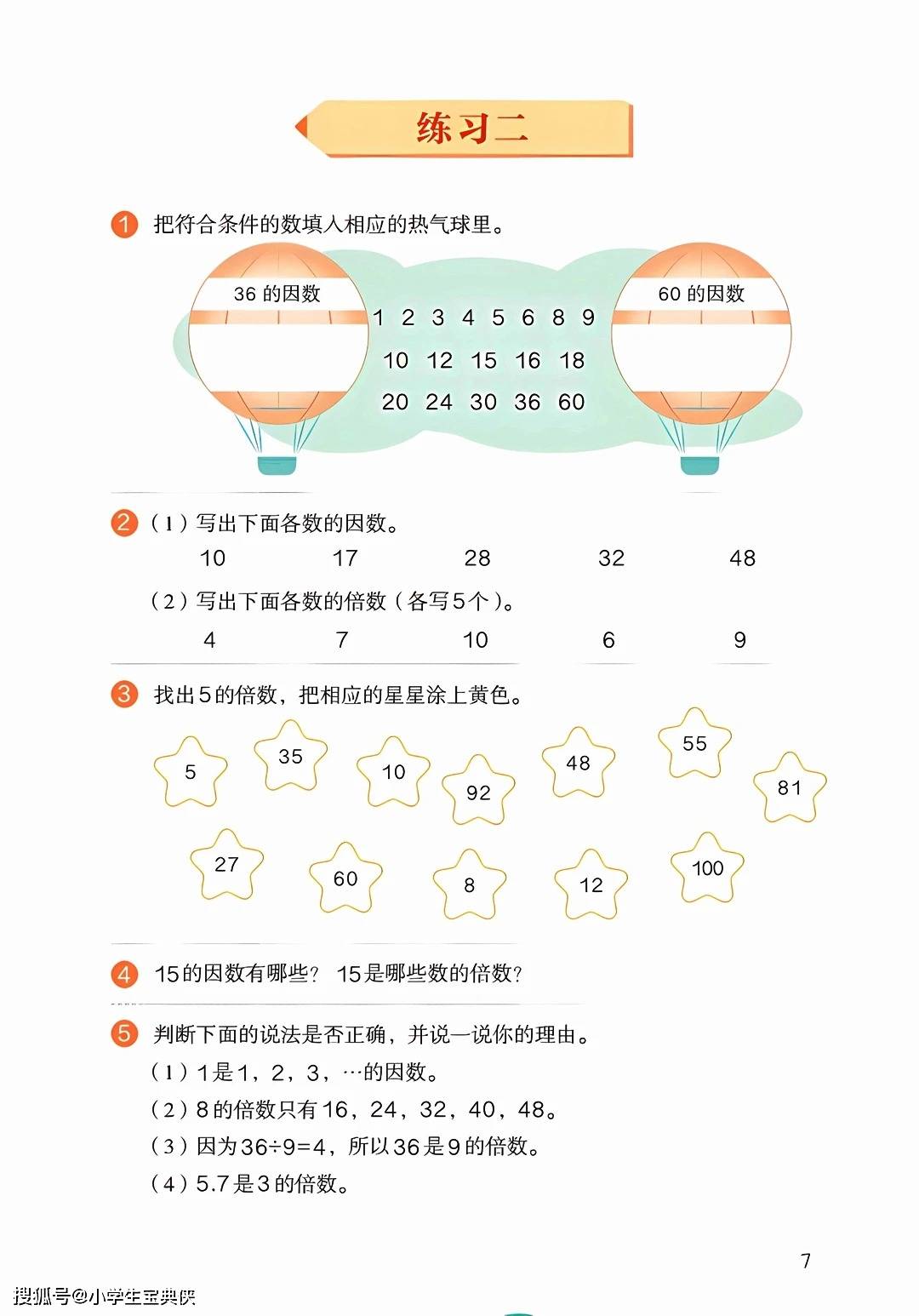
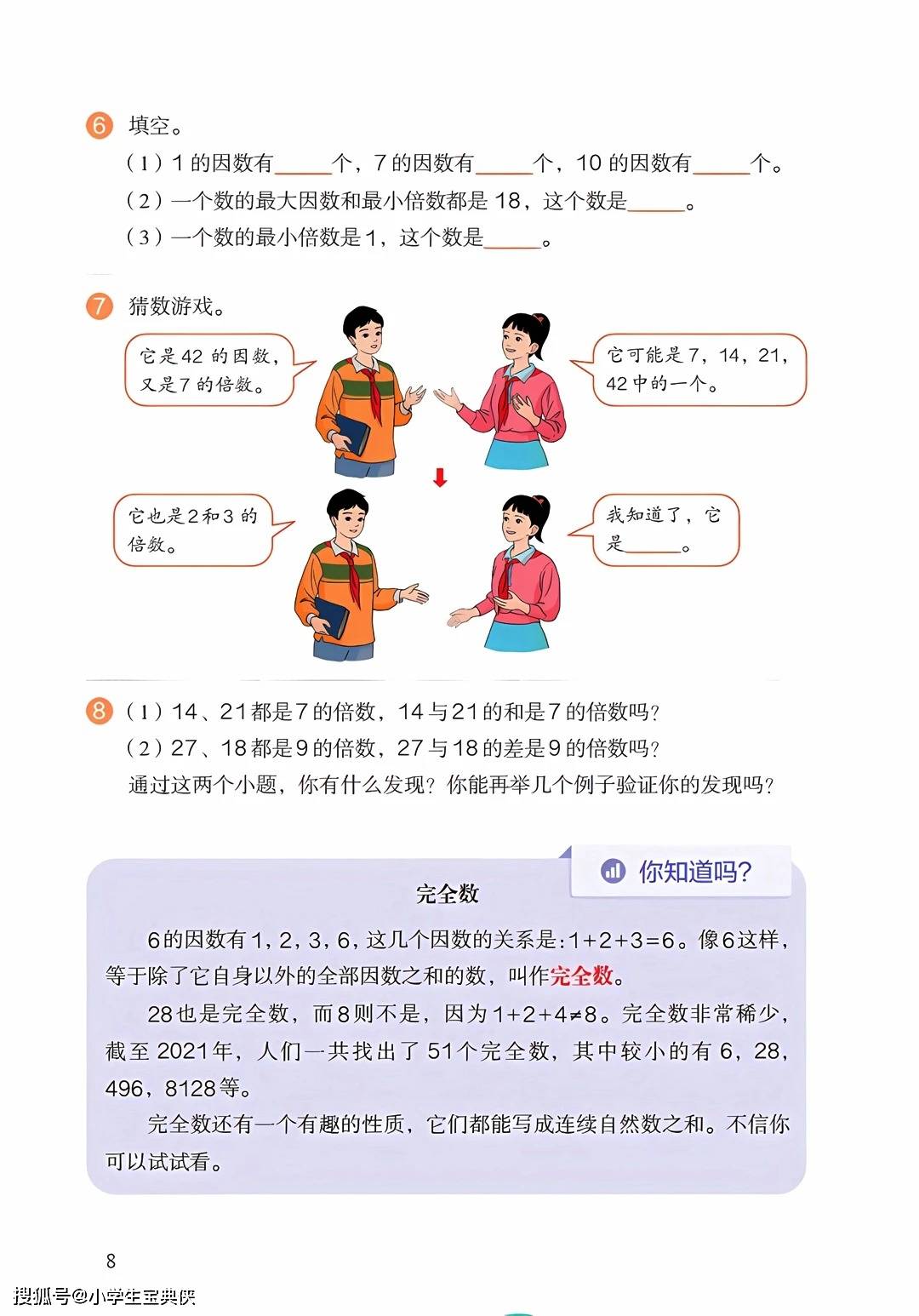
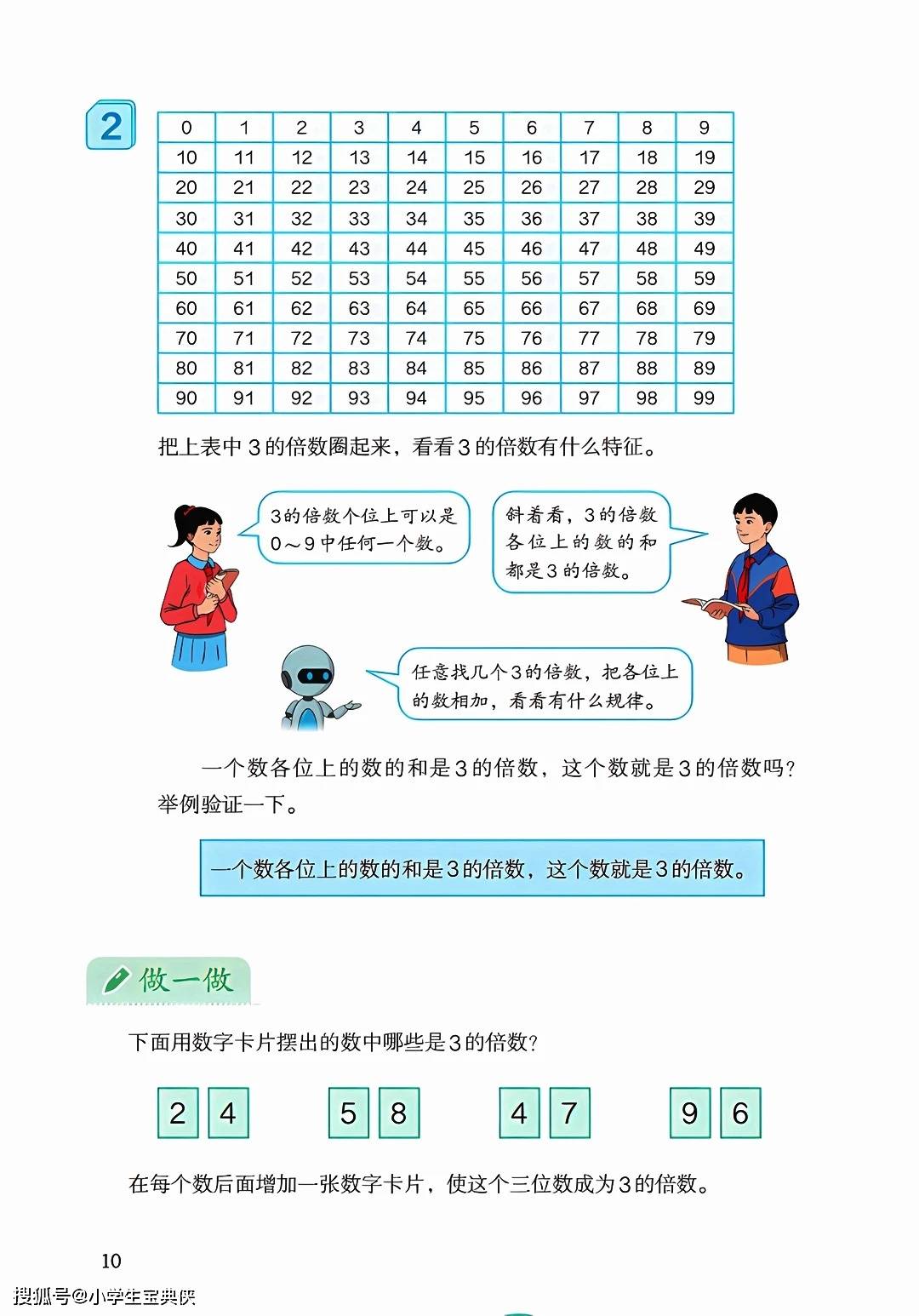
因数和倍数是数与代数领域的重要基础。教材通过整数除法引入因数和倍数的概念,指出在商为整数且没有余数的情况下,除数和商是被除数的因数,被除数是除数和商的倍数。找因数的方法是从 1 开始依次试除,而找倍数则是通过乘法得到。一个数的因数个数有限,倍数个数无限,最小倍数和最大因数都是它本身。
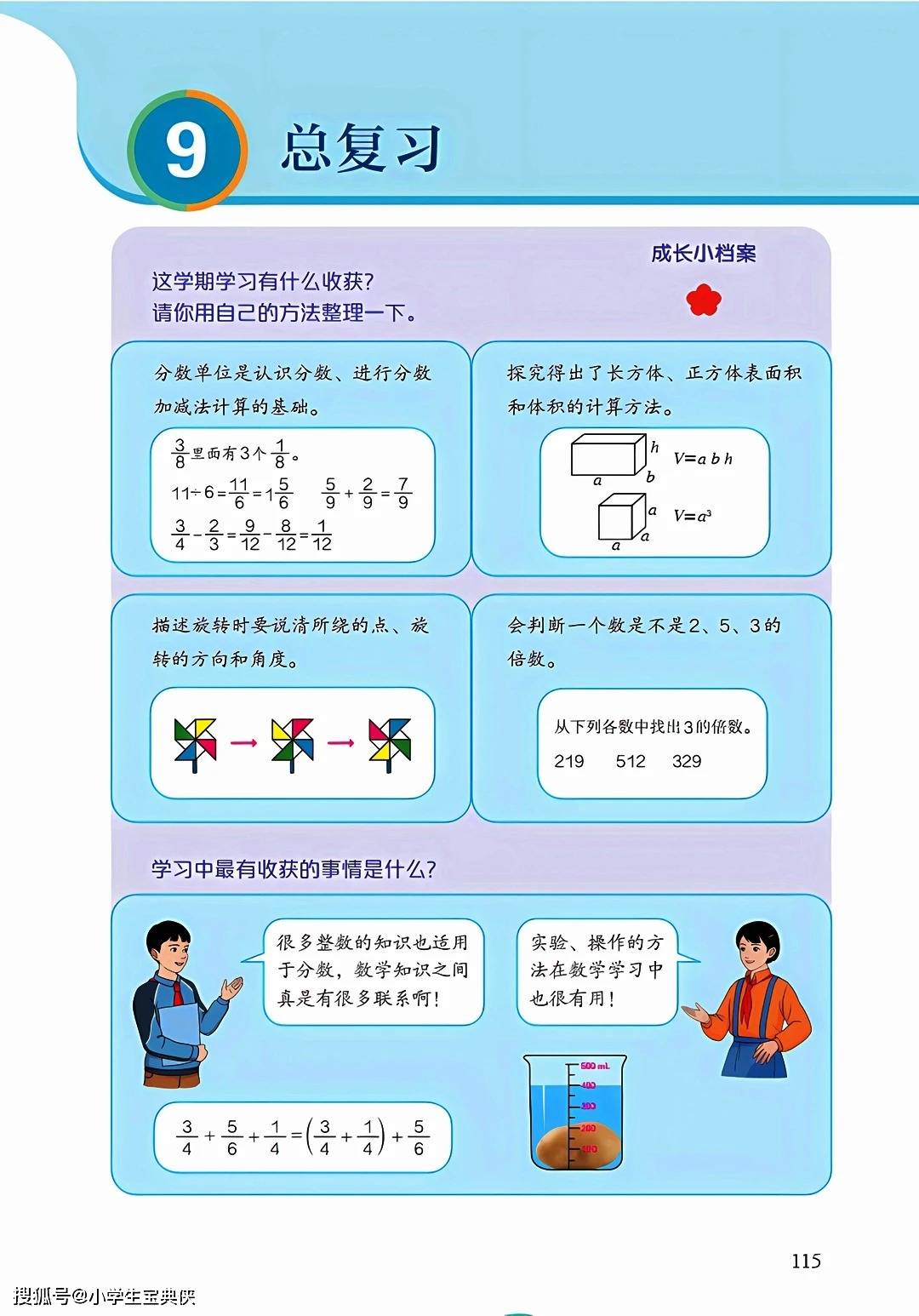
长方体和正方体是本册教材中空间与图形领域的重点。学生需要认识这两种立体图形的基本特征,包括面、棱、顶点的数量和特点。长方体有 6 个面、12 条棱和 8 个顶点,相对的面和棱分别相等;正方体的 6 个面都是正方形,12 条棱长度相同。棱长总和、表面积和体积的计算是这一部分的核心内容。长方体的表面积公式为(长 × 宽+长 × 高+宽 × 高)×2,体积公式为长 × 宽 × 高;正方体的表面积公式为棱长 × 棱长 ×6,体积公式为棱长 × 棱长 × 棱长。容积的计算方法与体积相同,但测量数据需来自容器内部。
探索图形是在认识长方体和正方体之后的拓展内容,通过观察由小正方体组成的大正方体表面涂色情况,寻找其中的规律。学生需要分析不同位置的小正方体被涂色的面数,从而总结出一般性的规律,培养观察和归纳能力。
分数的意义和性质是本册教材的另一个重点。教材首先通过单位 “1” 的平均分引入分数的概念,指出分数表示其中的一份或几份。分数单位是表示一份的数。分数与除法存在对应关系,被除数除以除数等于分数形式。分数的基本性质指出,分子和分母同时乘或除以同一个不为 0 的数,分数大小不变。约分和通分都是基于这一性质进行的操作,约分是将分数化为最简形式,通分则是将异分母分数化为同分母分数,以便进行比较和运算。
图形的运动(三)主要学习图形的旋转。旋转由旋转中心、旋转方向和旋转角度三个要素决定。图形在旋转过程中,形状和大小保持不变,只是位置发生变化。对应点到旋转中心的距离相等,对应线段的夹角等于旋转角度。学生需要掌握如何根据给定的旋转条件画出旋转后的图形。
分数的加法和减法包括同分母分数相加减和异分母分数相加减。同分母分数相加减时,分母不变,分子相加减;异分母分数相加减时,需要先通分,再按照同分母分数的法则计算。分数加减混合运算的顺序与整数相同,有括号先算括号内,无括号从左到右依次计算。折线统计图部分介绍了单式和复式两种折线统计图。折线统计图不仅能表示数量的多少,还能清晰地反映数量的变化趋势。复式折线统计图可以同时展示两组或多组数据的变化情况,便于比较。绘制折线统计图的步骤包括描点、连线和标注数据。
数学广角 —— 找次品的内容主要讨论如何用最少的次数在若干物品中找出质量不同的次品。基本策略是将物品分成三份,每份数量尽量平均,通过天平称重的结果逐步缩小次品所在的范围。这一过程需要逻辑推理和优化思想。人教版五年级下册数学教材的知识点分布较为均衡,既注重基础知识的巩固,又强调数学思维的培养。通过对这些内容的学习,学生能够进一步发展空间观念、数感、运算能力和统计意识,为后续的数学学习奠定基础。
