2026年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2026新苏教版三年级数学（下册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

如需全套电子课本PDF版，请关注公众号“桃李科普”回复：“电子课本”

苏教版三年级数学（下册）-电子课本在线阅读

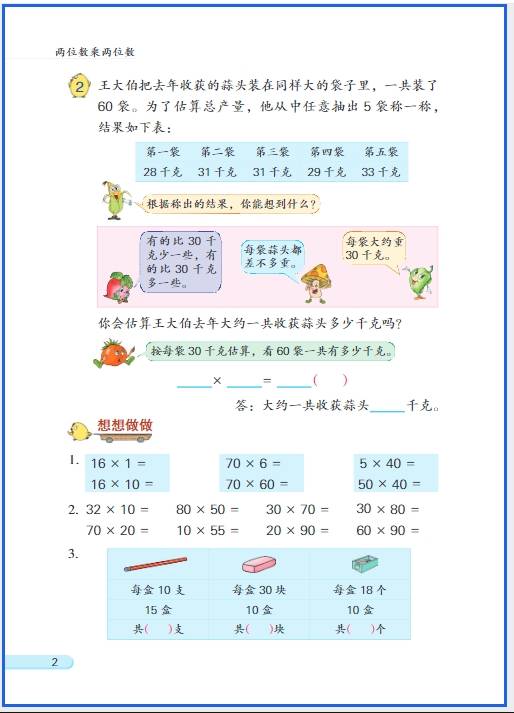
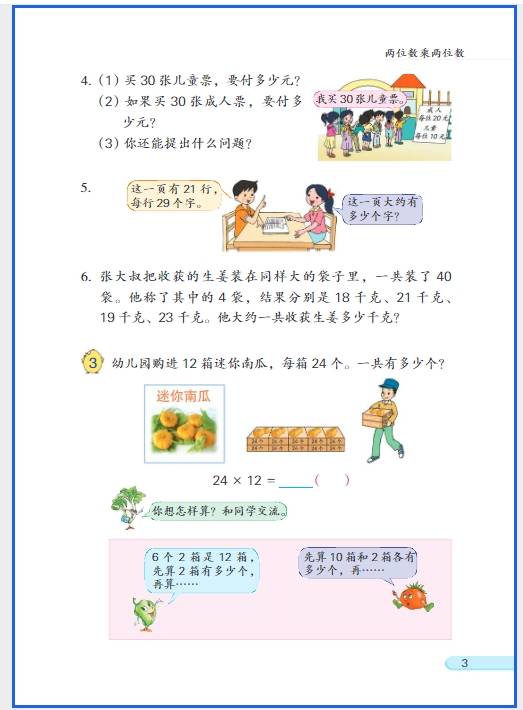
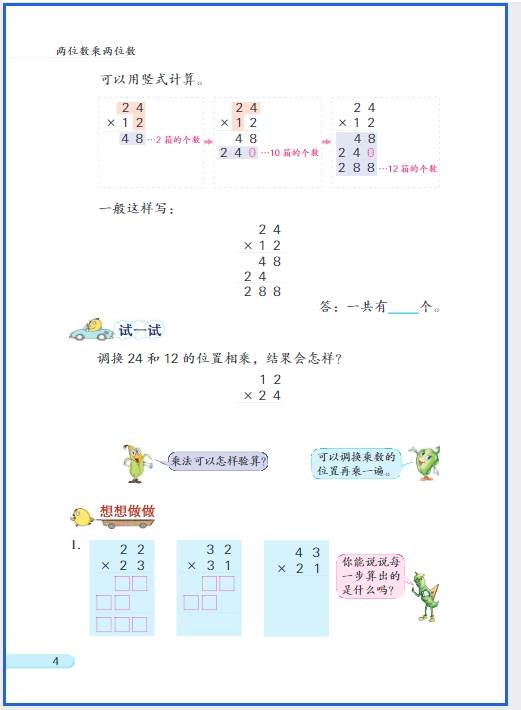
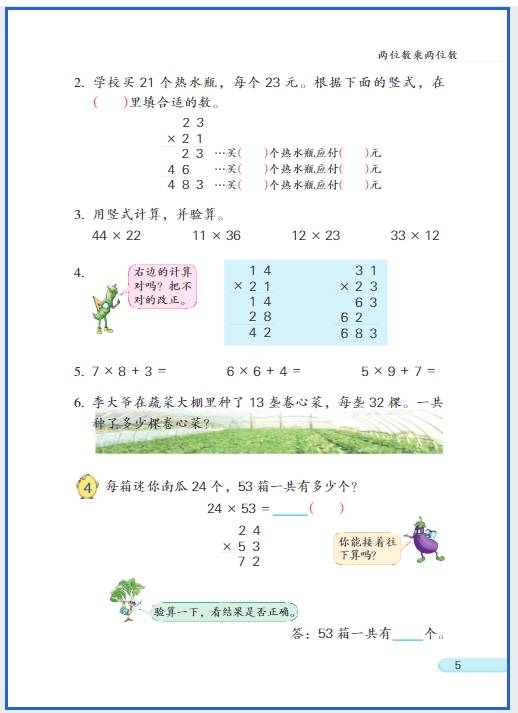
三年级数学思维训练的核心是在夯实基础的前提下，培养逻辑推理、数形结合、逆向思考等能力，重点围绕 “运算拓展、图形认知、应用题逻辑、排列组合” 四大方向展开，以下是分模块的训练内容和方法，适配教学与辅导场景：

一、运算类思维训练（提升计算灵活性）

1. 巧算与速算（突破常规计算，培养凑整意识）

• 核心方法：
• 凑整法：利用加法交换律、结合律，减法的性质凑整（如 \(298+156=300+156-2=454\)；\(567-199=567-200+1=368\)）。
• 乘法分配律初步：针对多位数乘一位数的简便计算（如 \(12×5=(10+2)×5=10×5+2×5=60\)；\(99×3=(100-1)×3=300-3=297\)）。
• 连乘 / 连除巧算：如 \(25×4×6=100×6=600\)；\(360÷6÷5=360÷(6×5)=12\)。
• 训练例题：① 计算 \(305+297+196\)；② 计算 \(456-102-98\)；③ 计算 \(125×8×3\)。

2. 数字谜（培养逆向推理和数位意识）

• 核心题型：
• 加法 / 减法竖式谜：根据已知数字推导未知数字，需结合进退位规则（如：plaintext
• □ 3 □
• + 2 □ 6
• --------
• 5 0 1
• 推导：个位\(□+6=1\)，说明有进位，个位是 5；十位\(3+□+1=10\)，十位是 6；百位\(□+2+1=5\)，百位是 2）。
• 乘法竖式谜：结合多位数乘一位数的进位规则（如 \(□2×3=126\)，推导得十位为 4，即\(42×3=126\)）。
• 训练要点：从个位或有确定数字的数位入手，结合进退位反向推导。

二、图形类思维训练（强化空间感知与转化能力）

1. 周长的进阶计算（突破常规公式，学会 “转化法”）

• 核心题型：
• 不规则图形周长：通过平移线段转化为长方形 / 正方形（如 “阶梯状” 图形，平移后周长等于长加宽的和乘 2）。例：求下图周长（单位：cm）plaintext
• ┌───────┐
• │ │
• │ ┌───┘
• │ │
• └───┘
• （长5cm，宽3cm，平移后周长=(5+3)×2=16cm）
• 拼组图形周长：多个正方形 / 长方形拼大图形，分析周长变化（如 2 个边长为 2cm 的正方形拼长方形，周长减少 2 条边长，即\(2×4×2 - 2×2=12cm\)）。
• 训练要点：抓住 “周长是封闭图形一周的长度”，通过平移、拼接转化为熟悉图形。

2. 图形计数（培养有序思维，避免重复 / 遗漏）

• 核心题型：
• 数长方形 / 正方形个数：按 “从小到大” 或 “按行 / 列” 分类计数（如：由 1 个小正方形组成的：4 个；由 4 个小正方形组成的：1 个；总计 5 个正方形）。
• 数线段 / 角的个数：用公式 “\(n(n-1)÷2\)”（n 为端点 / 射线数，如 5 个端点的线段数为\(5×4÷2=10\)）。
• 训练例题：数出下图中长方形的个数（提示：先数长的线段数 × 宽的线段数）。

三、应用题类思维训练（提升逻辑分析与建模能力）

1. 归一 / 归总问题（建立 “单一量” 和 “总量” 的思维）

• 归一问题：先求 “单一量”，再求总量（如 “3 个苹果 15 元，买 8 个需要多少钱？” 先算 1 个苹果 5 元，再算 8×5=40 元）。
• 归总问题：先求 “总量”，再求单一量或份数（如 “小明每天看 6 页书，8 天看完，若每天看 8 页，几天看完？” 先算总量\(6×8=48\)页，再算\(48÷8=6\)天）。
• 训练要点：找准 “不变量”（归一的单一量、归总的总量）。

2. 和差 / 和倍问题（初步接触数量关系模型）

• 和差问题：已知两数和与差，公式 “大数 =(和 + 差)÷2，小数 =(和 - 差)÷2”（如 “甲乙两数和为 50，差为 10，求两数”，大数 =(50+10)÷2=30，小数 = 20）。
• 和倍问题：已知两数和与倍数关系，公式 “小数 = 和 ÷(倍数 + 1)，大数 = 小数 × 倍数”（如 “甲乙和为 36，甲是乙的 2 倍，求甲乙”，乙 = 36÷(2+1)=12，甲 = 24）。
• 训练要点：通过画线段图直观表示数量关系。

3. 鸡兔同笼（初步接触假设法）

• 核心方法：假设全是鸡或全是兔，通过差值推导数量（如 “笼中鸡兔共 10 只，脚 28 只，求鸡兔各几只”：假设全是鸡，脚有\(10×2=20\)只，差\(28-20=8\)只，每只兔比鸡多 2 只脚，故兔有\(8÷2=4\)只，鸡有 6 只）。
• 训练要点：用 “假设 - 找差 - 调整” 的步骤解题，可结合画图辅助理解。

四、逻辑与组合类思维训练（培养有序和推理能力）

1. 排列组合（强化有序枚举）

• 核心题型：
• 数字搭配：用 1、2、3 组成无重复的三位数，按百位分类枚举（1 开头：123、132；2 开头：213、231；3 开头：312、321，共 6 个）。
• 搭配问题：3 件上衣和 2 条裤子，共\(3×2=6\)种搭配方式；路线问题（A 到 B 有 2 条路，B 到 C 有 3 条路，A 到 C 共\(2×3=6\)条路）。
• 训练要点：按 “分类 - 枚举 - 计数” 的步骤，避免重复或遗漏。